パスカルの三角形 Wikipedia 端的に言うと パスカルの三角形の行の各数字を求めることと、二項係数の係数を求めることは同じことをしている からです。 以下、長ったらしいので読まなくていいです。 意味がわからないと思うので順を追って説明していき対象商品 ︎ルーローの三角形 (数学的木のおもちゃ 知育玩具 木育) ¥3,0 残り4点 ご注文はお早めに この商品は、木のおもちゃ製作所・銀河工房が販売し、Amazon Fulfillment が発送します。 通常配送無料(一部の商品・注文方法等を除く) 詳細 ︎三丁目 パスカルの三角形 歴史と名称 朱世傑の四元玉鑑(1303年)における楊輝の三角形 『永楽大典』巻(1408年)より。楊輝は賈憲(英語版)の『釈鎖算書』中の「パスカルの三角形」を引用した。この三角形について確認
パスカルの三角形の不思議な性質7個 パスカルの三角形に秘められた不思議な性質 やまでぃーのブログ
パスカルの三角形 (a+b)6
パスカルの三角形 (a+b)6- a^6b^6=(ab)^6 – 6a b(ab)^4 9(a b)^2(ab)^2 2(a b)^3 となります.パスカルの三角形恐るべしです. カテゴリー パスカルの三角形 、 対称式 、 数学 、 未分類 投稿ナビゲーション綾瀬個別指導学院 糸井です。 今回は、 パスカルの三角形 を紹介します。これを知っていると、 二項展開 するときに役立ちます。 ともに係数が1である 二項式 の累乗を 展開 し、各項の 係数 だけを取り出して順に並べると、図のような三角形になります。この三角形を「 パスカルの三




Python演算処理 パスカルの三角形と二項定理または二項展開 Qiita
パスカルの三角形 Pascal's triangle パスカルの三角形の性質 パスカルの三角形には色々な性質を持っています。 本ページではその中からいくつかを紹介します。 パスカルの三角形の作り方 パスカルの三角形の作り方は非常に単純なルールに基づいています。 まず1段目と各段の両端に1を置きます。 そしてその他の数は左上と右上の数の和を置きます。 例えば3段目パスカルの三角形の最初の6段 パスカルの三角形の計算法 また、それぞれの二項係数は wパスカルの三角形 (英:Pascal's triangle)と呼ばれる方法でも計算することができる。 実際は(ab)^7 になるとパスカルの三角形はドンドン高くなる一方ですね。 果てしなく東京のビルディングみたいに。 ・最終的な問題は 最初はパスカルの三角形の応用からで、こんどパスカルの三角形を使わずどう展開するかです。
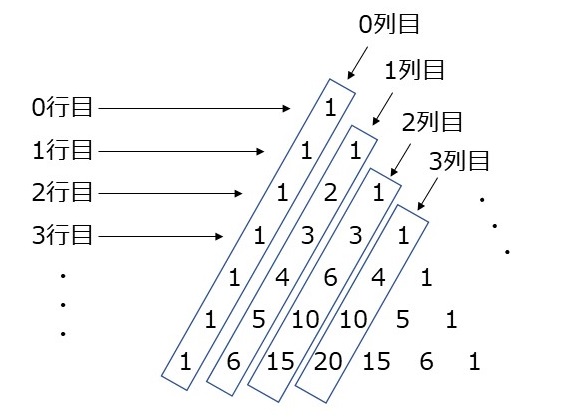
三角形 パスカルの三角形 c言語, recursive call パスカルの三角形とは次のような数表のことです。 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 各値は上の左右の値を足したものになっています。 そして、その値は組合せの数を表しています。パスカルの三角形は、 ( a b) n を展開したときの係数を書きだした表で、 右のようなものになります。 上の段の数字を足していくだけなので、簡単に作成することができます。 一番外側の数字は必ず1です。 二項定理 では、係数を1項ずつ計算する必要 この数の三角形がパスカルの三角形と呼ばれているのは、パスカル Pascal, Blaise, が1654年から1658年頃までの間に書いたとされる一連の論文において算術三角形を計算原理とした数列の計算法や二項展開法を整理するとともに組み合わせ論、確率論の基礎を確立し、その後の理論の発展の
重複組合せとパスカルの三角形 「10 個のりんごをa,b,c の3 人が分ける方法は何通りあ るか.ただし,1 個ももらわない人がいてもよいものとする」 という重複組合せの問題がある. 授業では,「10 個の とa,b,c を区切る2 つの/を並べるパスカルの三角形の最初の6段 この三角形の作り方は単純なルールに基づいている。 まず最上段に 1 を配置する。 それより下の段は両端には 1 を、それ以外の位置には右上の数と左上の数の和を配置する。 例えば、5段目の左から2番目には、左上の 1 と右上の 3 の合計である 4 が入る。 このようにして数を並べると、上から n 段目、左から k 番目の数は、 二項パスカルの三角形は、(a+b)nの展開に利用される。 (a+b)2=a2+2ab+b2=1a2+2ab+1b2 (a+b)3=a3+3a2b+3ab2+b3=1a3+3a2b+3ab2+1b3 この性質を利用すると、いちいち分配法則を用いることなく、一気に式が展開できる。 たとえば、(a+b)5を展開したい場合、パスカルの三角形から、 1 5 10 10 5 1 が直ぐ得られるので、 (a+b



パスカルの三角形と数列
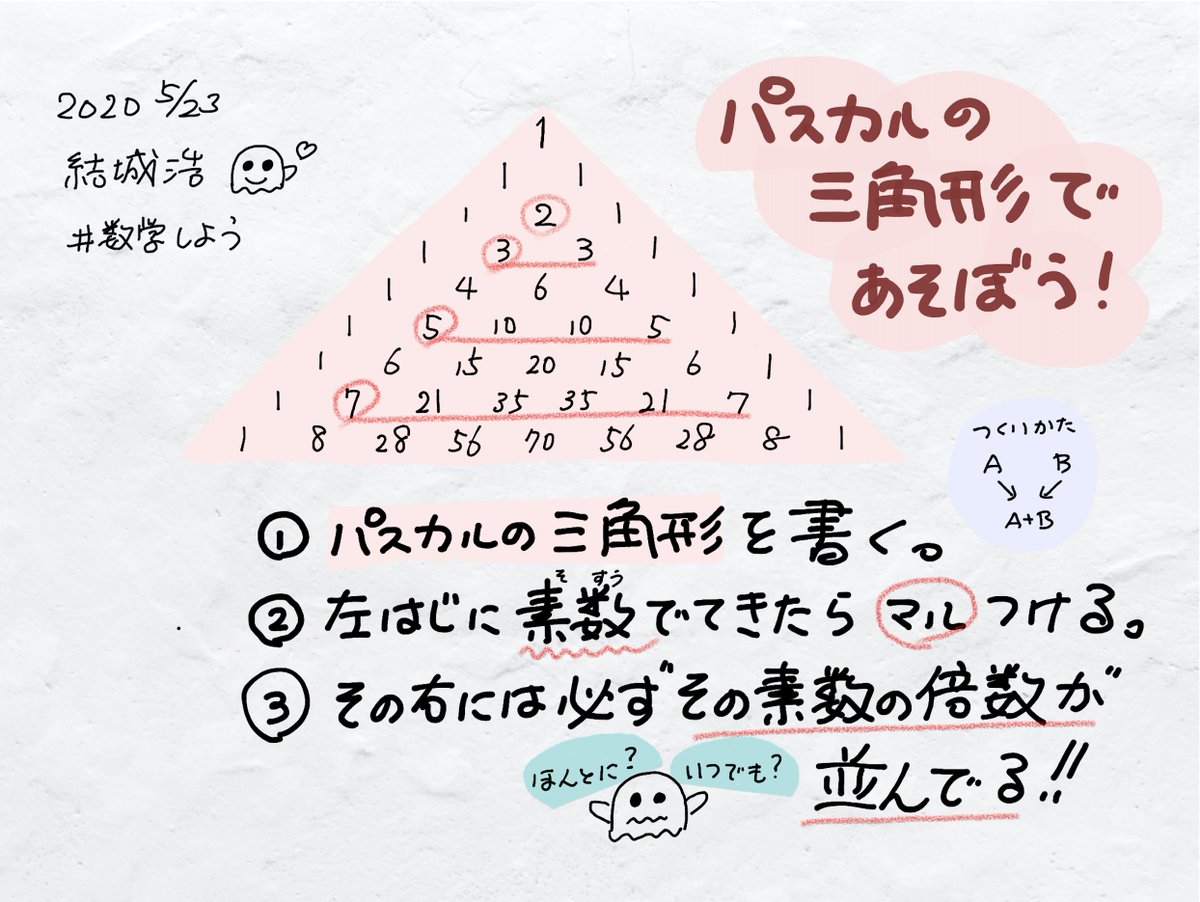



結城浩 Twitterissa パスカルの三角形であそぼう パスカルの三角形を書く 左端に素数が出てきたらマルをつける その右には 必ず その素数の倍数が並んでる 両端の1は除いてね 数学しよう
パスカルの三角形とは,図のように数字が三角の形にならんでいるもののこと。 知らない人が見たら,一見恋愛のおまじない(占い?)に見えるかも。 その成り立ちは,ご覧の通り,左下と右下にわかれながら,足されて次の段が 作られる。 SICP遅々と読む。練習問題にパスカルの三角形の要素を計算せよ(再帰を使って)、というのがある。 フィボナッチ数列の次くらいに手軽な題材でいろいろ試せて遊べるなと。 Clojureらしい解き方は、やっぱ遅延シーケンスを作るやり方だろうなと。 出力形式は問われていないから、任意二項定理において,a=1,b=1とすると,パスカルの三角形において,各段の数の総和がすぐに分かる。 例えば,(1+1) 4 =1 4 +4 3 ×1 1 +6 2 ×1 2 +4×1 3 +1 4 だから 1+4+6+4+1=2 4 =16 また,二項定理において、a=10,b=1とすれば,次のような性質も成り立つ。




Python演算処理 パスカルの三角形と二項定理または二項展開 Qiita




15年9月のブログ記事一覧 4ページ目 身勝手な主張
パスカルの三角形の、一つの行にあるすべての数をそれぞれ2乗して和をとると、ある行の真ん中にある数になることに気付きました。 ↓はパスカルの三角形です 1 11 121 1331 1 6 15 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 では一つの行にある数をそれぞれ2乗し、足し合わせようと思い パスカルの三角形までは求められたのですが、(ab)6乗の展開式が求められません! 教えてください💦 (Z十の* の展開式の係数を次々 件 人 2三1 ま。 ある数がパスカルの三角形に出現する回数を数えるプログラムを高速化して3003が8回出現するところまで確認する 週末、18年の数学系アドベントカレンダーを読もうと思って 日曜数学 Advent Calendar 18 を眺めていたら1日目から早速tsujimotterさんの面白い記事



パスカルの三角形の問題です 数学高校入試問題です どなたか解いてもらえません Yahoo 知恵袋




Python演算処理 パスカルの三角形と二項定理または二項展開 Qiita
これを、パスカルの三角形(正方形! ? )に翻訳(ほんやく)するのに、 a というのを 道で上にいくこと b というのを 道で横にいくこと と考えると、 (a+b)(a+b)(a+b) というのは、1歩ごとに上へ行こうか右に行こうかと考えながら3歩いくパスカルの三角形に潜む母関数 1 横の列 図のように、パスカルの三角形の横の数列は、(1+x) n のx k の各係数になっています。 これは高校でも教える内容です。パスカルの三角形とは、最上段に1 を配置し、 それより下の段に右上の数と左上の数の和を置いた三角形のことである。 これは二項定理と深い関わりがあり、パスカルの三角形の n 段目に対して、(ab) n1 の係数が対応している。



6 二項定理 ノート ひまわり数学教室



二項定理とは 公式と係数の求め方 応用までをわかりやすく解説
二項式を取り、(a b)それを3乗すると、が得られa^3 3a^2b 3ab^2 b^3ます。パスカルの三角形は、二項式展開の各項の係数を表したものです。二項式を上げるための累乗は、係数が入っている線を上から表します。パスカルの三角形の構成方法を説明するために,次のような記号を導入しよう。上から第n行目,左から第r番目の数をa (n,r) と表す。nは負でない整数,rは0からnまでの整数の範囲を動く。図2は,このa (n,r) を並べたものである。パスカルの三角形は,次の 答えはa=c=0です。 解答は、展開して、有理数と√6の係数が共に0の連立方程式を立てた後、2aq^29ar^2c=0かつ6aq^23ar^2c=0ー①からcを消去して、a≠0と仮定して、6r^2=4q^2から√6=2q/rで矛盾を示しています。 自分の解答は、①までは同じですが、そこから①⇆8aq^2c=0かつ12ar^2c=0ー②から、a=0のとき②⇆c=0 a≠0のとき②⇆q^2=c/8aかつr^2=




A B が A 4a B 6a B 4ab B Clear




Tossランド 二項定理 の基礎 基本
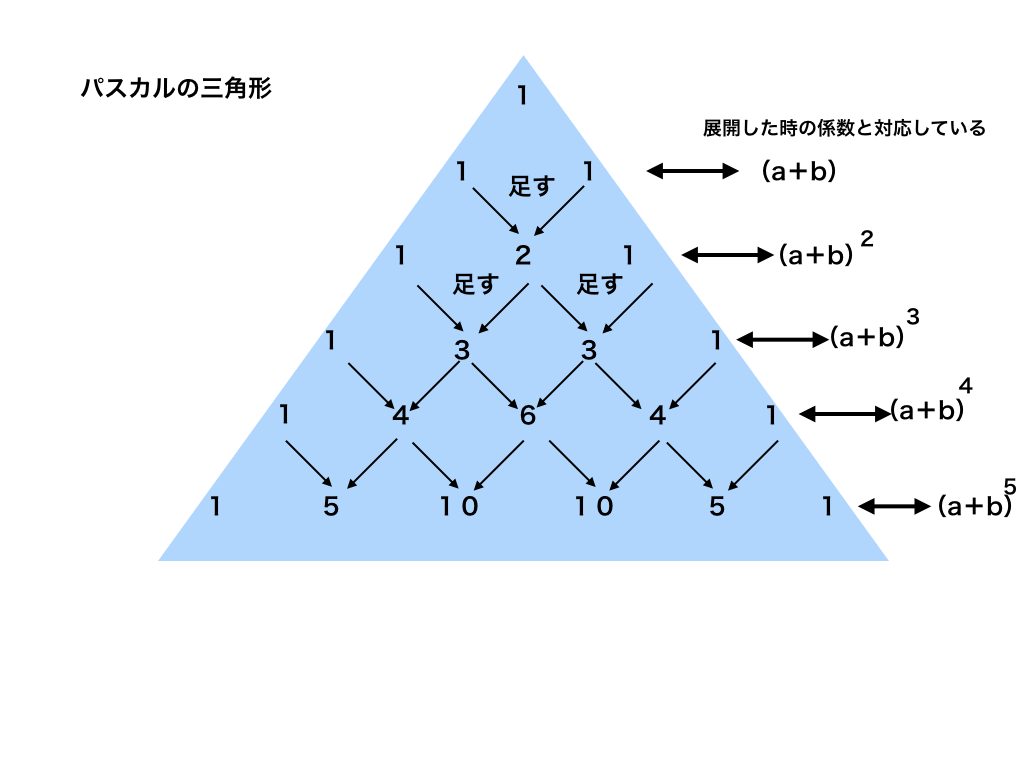
パスカルの三角形を利用した計算 パスカルの三角形は以下の図の通りです。 1 上段から順に、横並びの2数の和を1段下に記述していくことで作成できます。 組み合わせ計算の結果に対応することが知られていますので、これを利用します。 プログラム つまり、 パスカルの三角形に出てくる n 段目の数字は、 n 乗を展開したときの係数を表す ことになります。 そのため、2段目の数字が「 1 2 1 1 2 1 」となっていることと (x y)2 = x2 2xy y2 ( x y) 2 = x 2 2 x y y 2 となることが対応しています。 また、5段目の パスカルの三角形の使い道 それでは、このパスカルの三角形というものが どういった場面で役に立つのか、それは 展開公式の係数を調べることができる! という点です。 例えば、\((ab)^4\)の展開を考える場合 パスカルの三角形の5段目を見ると



パスカルの三角形が二項係数になるのはなぜですか Quora



2
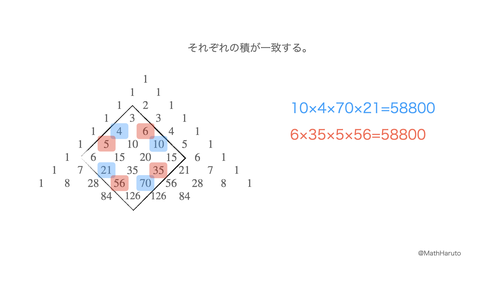
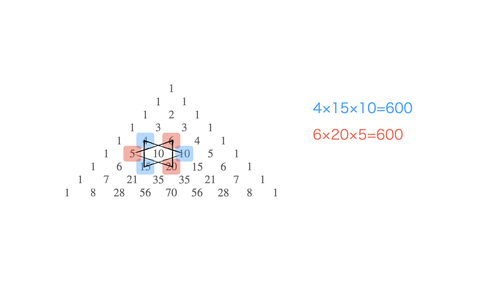
端の1を除いて,パスカルの三角形に含まれる数は6個の数で囲まれている.たとえば,6段目の10の回りには4,6,10,,15,5が取り囲んでいる. 4 6 5 10 10 15 6個のうち隣接しない3数の積はもう1組の隣接しない3数の積に等しい.この性質には「ダビデの星パスカルの三角形の中に現れる数を 倍数などに着目して色を塗り,規則 的な模様を見つける。 ・パスカルの三角形の きまりについて多面的 に捉え,筋道を立てて 考えたり表現したりして いる。 令和2年度版『小学 算数6』年間指導計画・評価計画(案) これは縦方向だけの単位数列をもとに、パスカルの三角形と同じように、対角線を超えない範囲で、公式 n C r = n-1 C r-1 + n-1 C r の関係を満たしながら作られている。 この三角形の一般項を求めようと思った。



2




ブレーズ パスカル Wikipedia
これらはk-パスカル三角形の第3段目に一致していた。 1 3 3 1 1 3 6 7 6 3 1 1 3 6 10 12 12 10 6 3 1二項展開への応用 パスカルの三角形のもっとも簡単な応用は 二項展開 です.これはつぎの 二項定理 に基づいています. 二項定理: (x y)n = n ∑ k=0nCkxkyn−k ( x y) n = ∑ k = 0 n n C k x k y n − k これより, (xy)n ( x y) n を展開したときの各項の係数は,二項係数になります.特に,展開の結果を知るには, nC0,⋯,nCn n C 0, ⋯, n C n の値をすべて知れば十分です. この公式こそが,パスカルの三角形を斜めに見るとフィボナッチ数列が浮き上がってくる理由の説明になります.ここで $$\binom{nk}{k}$$ という二項係数は, (\cos n\theta) の表示 で紹介した, (a^nb^n) を基本対称式で表すときに用いた形式的冪級数を求める際に似たような式が出てきたのを思い出してください.




パスカルの三角形の不思議な性質7個 パスカルの三角形に秘められた不思議な性質 やまでぃーのブログ



Www Chiba C Ed Jp Shidou K Kenkyu H23 Suugaku 5 Pdf
たまには数学ネタを。 数学Ⅱの教科書で出てくるパスカルの三角形。 それが、(ab)^n を展開した時の各項の係数を表しているんだけど、それを説明するのに、 (ab)^3を展開させます。 その時に、わざと(ab)(ab)^2として、縦に同類項が並ぶように2行使って書いて、係数が 1 3 3 1 になることを右のようにピラミッド状に並んだ数をパスカルの三角形という。 これは上の段の数字がわかると、下の段の数字がわかるようになっている。 この法則を発見し、(ab)6 の展開式を求めよ。 (a b)6 = ×a6 ×a5b ×a4b2 ×a3b3 ×a2b4 ×ab5 ×b6パスカルの三角形拡張 今、2つの項をもつ式を次数を上げながら展開していきます。 (ab) 1 = a b (ab) 2 = a 2 2ab b 2 (ab) 3 = a 3 3a 2 b 3ab 2 b 3 (ab) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 (ab) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5




仮称 パスカルの逆数三角形 完全無欠で荒唐無稽な夢




二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ



A B の6乗と A B の5乗をパスカルの三角形を使って解いてく Yahoo 知恵袋



Python演算処理 パスカルの三角形と二項定理または二項展開 Qiita



二項定理とは 証明や応用問題の解き方をわかりやすく解説 受験辞典




パスカルの三角形までは求められたのですが A B 6乗の展開式が求められません 教 Clear
.jpg)



二項定理のしくみと意味 A B のn乗 高校数学なんちな




数 式と証明 二項定理は 箱からボールを選ぶ問題 として考える Mm参考書




Times 1 X1 6 2 2x 1 Descubre Como Resolverlo En Qanda



1




パスカルの三角形 Wikipedia
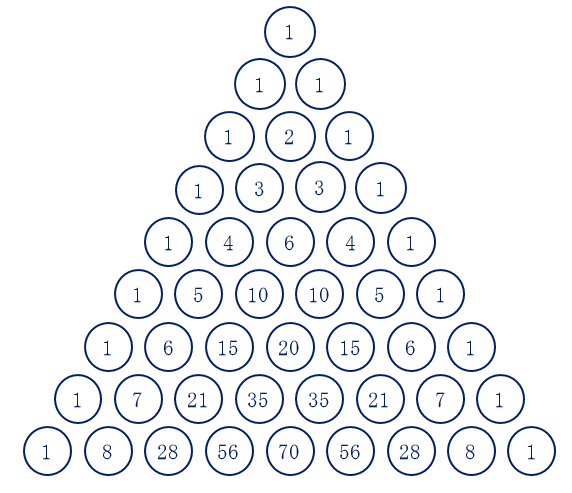



パスカルの三角形 パズルで鍛える発想力 中学受験プロ講師ブログ



It授業 実践ナビ 授業でitを使ってみませんか
.jpg)



二項定理のしくみと意味 A B のn乗 高校数学なんちな



ツバメの巣 Math 場合の数 二項定理
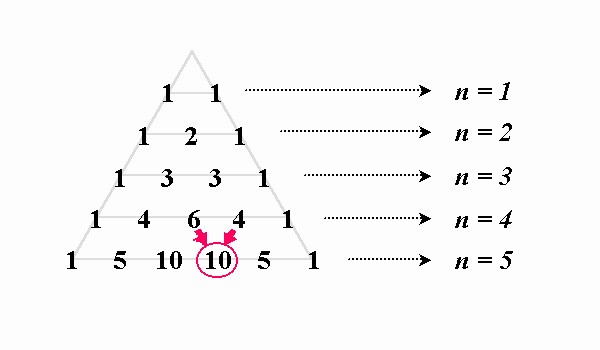



思索の散歩道 パスカルの三角形拡張




基本 N乗の展開とパスカルの三角形 なかけんの数学ノート



パスカルの三角形と最短経路 思考力を鍛える数学



パスカルの三角形と最短経路 思考力を鍛える数学
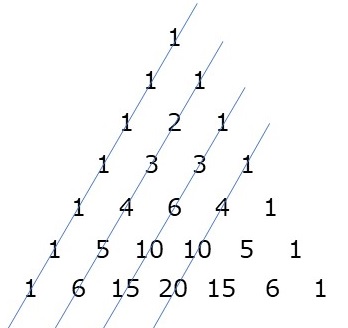



パスカルの三角形の不思議な性質7個 パスカルの三角形に秘められた不思議な性質 やまでぃーのブログ



パスカルの三角形




二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ



1




パスカルの三角形は 組合せ の母




パスカルの三角形 説明
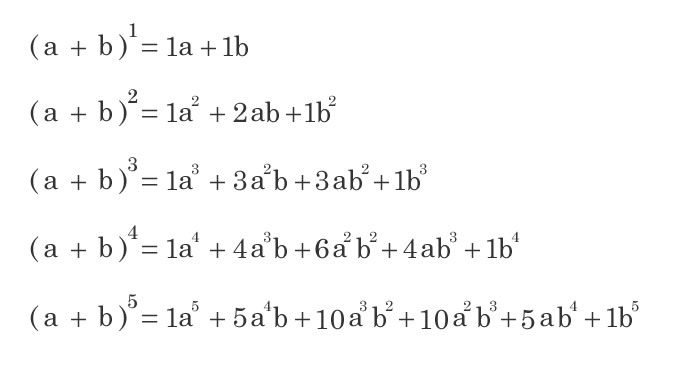



二項定理 パスカルの三角形 優技録




数2 展開と因数分解 パスカルの三角形 高校生 数学のノート Clear



Python演算処理 パスカルの三角形と二項定理または二項展開 Qiita



パスカルの三角形が二項係数になるのはなぜですか Quora



Clojureでパスカルの三角形 Programmer S Note




パスカルの三角形 時事用語事典 情報 知識 オピニオン Imidas イミダス




高校数学 数 ー4 パスカルの三角形 Youtube



2




どさにっき




パスカルの三角形 Wikipedia
.jpg)



二項定理のしくみと意味 A B のn乗 高校数学なんちな




二項定理のしくみと意味 A B のn乗 高校数学なんちな



数学 基礎 パスカルの三角形と展開公式の係数



二項分布




高校数学 二項定理 A B Nの展開式 整式の係数の和 受験の月
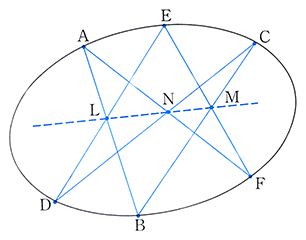



パスカルの定理とは コトバンク



パスカルの三角形の不思議 厳選 中学数学のおすすめ参考書




高校数学 数 2 パスカルの三角形 Youtube




すぐに忘れる脳みそのためのメモ Haskell でパスカルの三角形
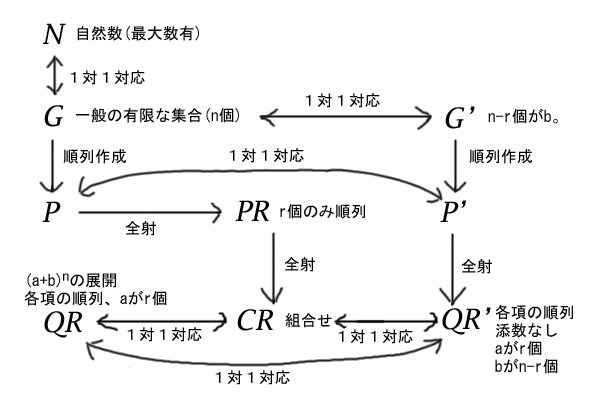



集合による二項定理と多項定理の証明とパスカルの三角形 高校数学マスター




結城浩 パスカルの三角形って フィボナッチ数列の親戚みたいですね
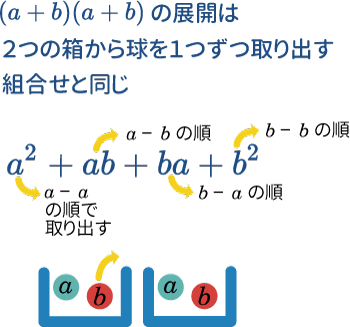



数 式と証明 二項定理は 箱からボールを選ぶ問題 として考える Mm参考書
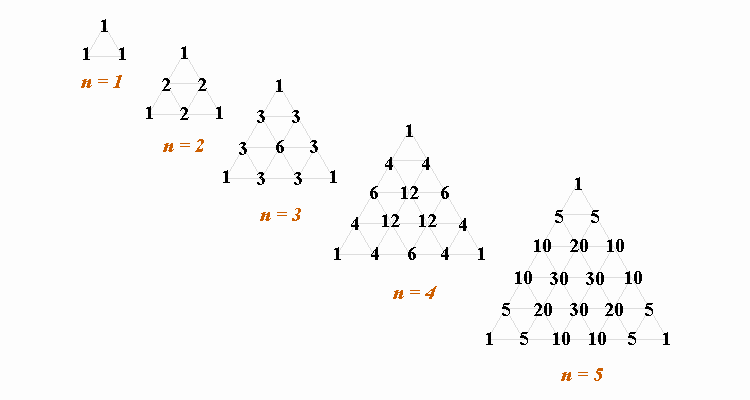



思索の散歩道 パスカルの三角形拡張



パスカルの三角形 さんすう 数学のお勉強




数 二項定理 パスカルの三角形 理由付き オンライン無料塾 ターンナップ Youtube



パスカルの三角形
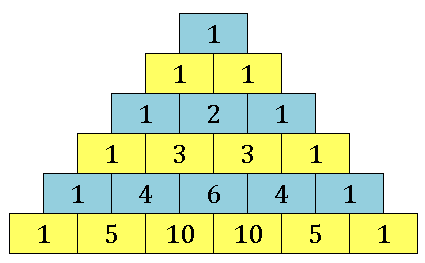



パスカルの三角形と 2 項定理 多項定理




Amazon Fr 新入試対応 数学ii B基礎問題精講 五訂版 Livres



1節 整式 分数式の計算 戻る 目 次 1章 式と証明 1節 式と計算 1 3次の乗法公式と因数分解 2 二項定理 3 整式の割り算 4 分数式とその計算 乗法公式や因数分解の苦手な人はここをクリック してください 高校2年で二項定理を学習します そのまえに




感じる科学 味わう数学 パスカルの賭け




二項定理のパスカルの三角形を利用する問題があるのですが Clear




パスカルの三角形 説明



2
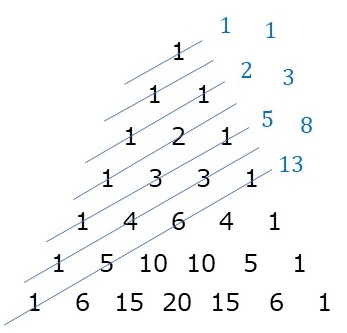



パスカルの三角形の不思議な性質7個 パスカルの三角形に秘められた不思議な性質 やまでぃーのブログ




高校数学 二項係数ncrの等式とパスカルの三角形 受験の月



パスカルの三角形と数列



N次元の三角形と パスカルの三角形 数が降る街



パスカルの三角形 Wikipedia




確率2 Unity学習帳




パスカルの三角形 説明
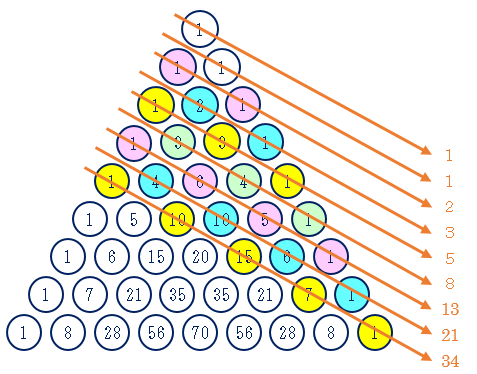



パスカルの三角形 パズルで鍛える発想力 中学受験プロ講師ブログ



パスカルの三角形



1




二項定理 ホモルーデンス



パスカルの三角形 Tomの日常



1



数学2bのパスカルの三角形について質問があります A 4bは4c1 A Yahoo 知恵袋




パスカルの三角形のプリントを改良しました 算数 数学専門塾 算数の極意




二項係数の公式3つをわかりやすく解説 2つの方法で証明します 遊ぶ数学
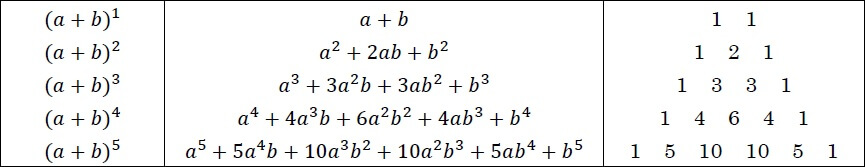



二項定理の公式と証明をわかりやすく解説 公式 証明 係数 問題



パスカルの三角形を利用して A B 6乗を展開せよこれを教えてくださ Yahoo 知恵袋



パスカルの三角形とシェルピンスキーギャスケット



2



パスカルの三角形



このもんだいの 2 3 のやり方をわかりやすく教えてください Yahoo 知恵袋




パスカルの三角形のポイントは4つ 中学受験 塾なし の勉強



2



文化祭00




パスカルの三角形と 2 項定理 多項定理



2
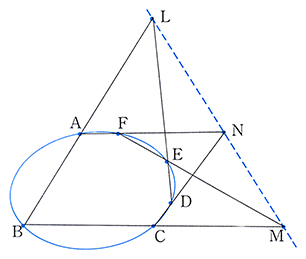



パスカルの定理とは コトバンク



2
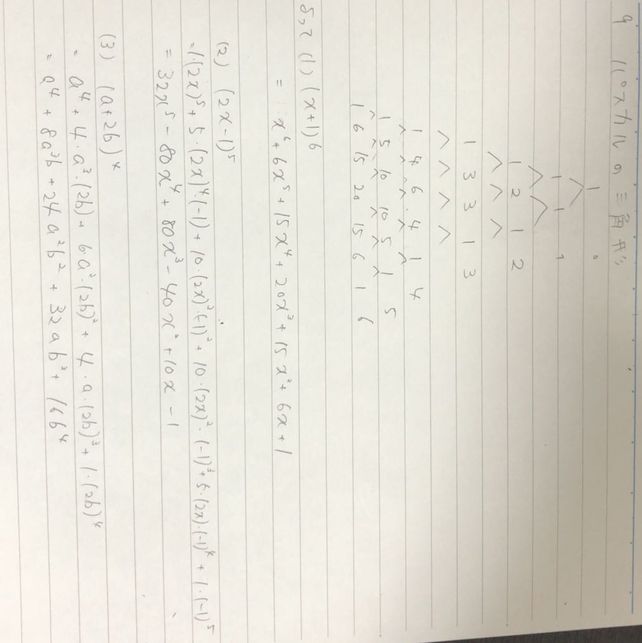



Times 1 X1 6 2 2x 1 Descubre Como Resolverlo En Qanda



0 件のコメント:
コメントを投稿