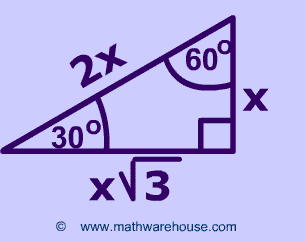
We can see that this must be a triangle because we can see that this is a right triangle with one given measurement, 30° The unmarked angle must then be 60° Since 18 is the measure opposite the 60° angle, it must be equal to $x√3$Right Triangle Calculator Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles , the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesIn a 30 60 90 special right triangle the hypotenuse is always equal to twice
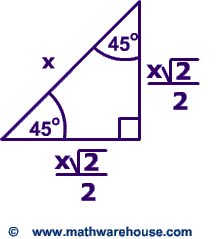
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
30 60 90 right triangle calculator
30 60 90 right triangle calculator-The triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X , turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at exactly 30On the other hand, sine has a value of 1 at 90° and 0 at 0°As a result, tangent is undefined whenever cos(θ)=0, which occurs at odd multiples of 90° (), and is 0 whenever sin(θ)=0, which occurs when θ is an integer multiple of 180° (π)The other commonly used angles are 30° (), 45° (), 60° and their respective multiplesThe




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above \(a^2b^2=c^2\) \(1^2(\sqrt3)^2=13=4=c^2\) \(\sqrt4=2=c\) Using property 3, we know that all triangles are similar and their sides will be in the same ratio When to use TrianglesTHE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that belowLearn how to solve for the sides in a Special Right Triangle in this free math video tutorial by Mario's Math Tutoring009 What are the Ratios of t
Trigonometry Examples Popular Problems Trigonometry Solve the Triangle tri {} {30} {} {60} {} {90} Side Angle b = c = a = A = 30 B = 60 C = 90 Side Angle b = c = a = A = 30 B = 60 C = 90 There is not enough information to solve for all of the sides and angles ofMath Warehouse's popular online triangle calculator Enter any valid combination of sides/angles(3 sides, 2 sides and an angle or 2 angle and a 1 side) , and our calculator will do the rest!A triangle is a special right triangle The other type of special right triangle is These numbers represent the degree measures of the angles The reason these triangles are considered special is because of the ratios of their sides they are always the same!
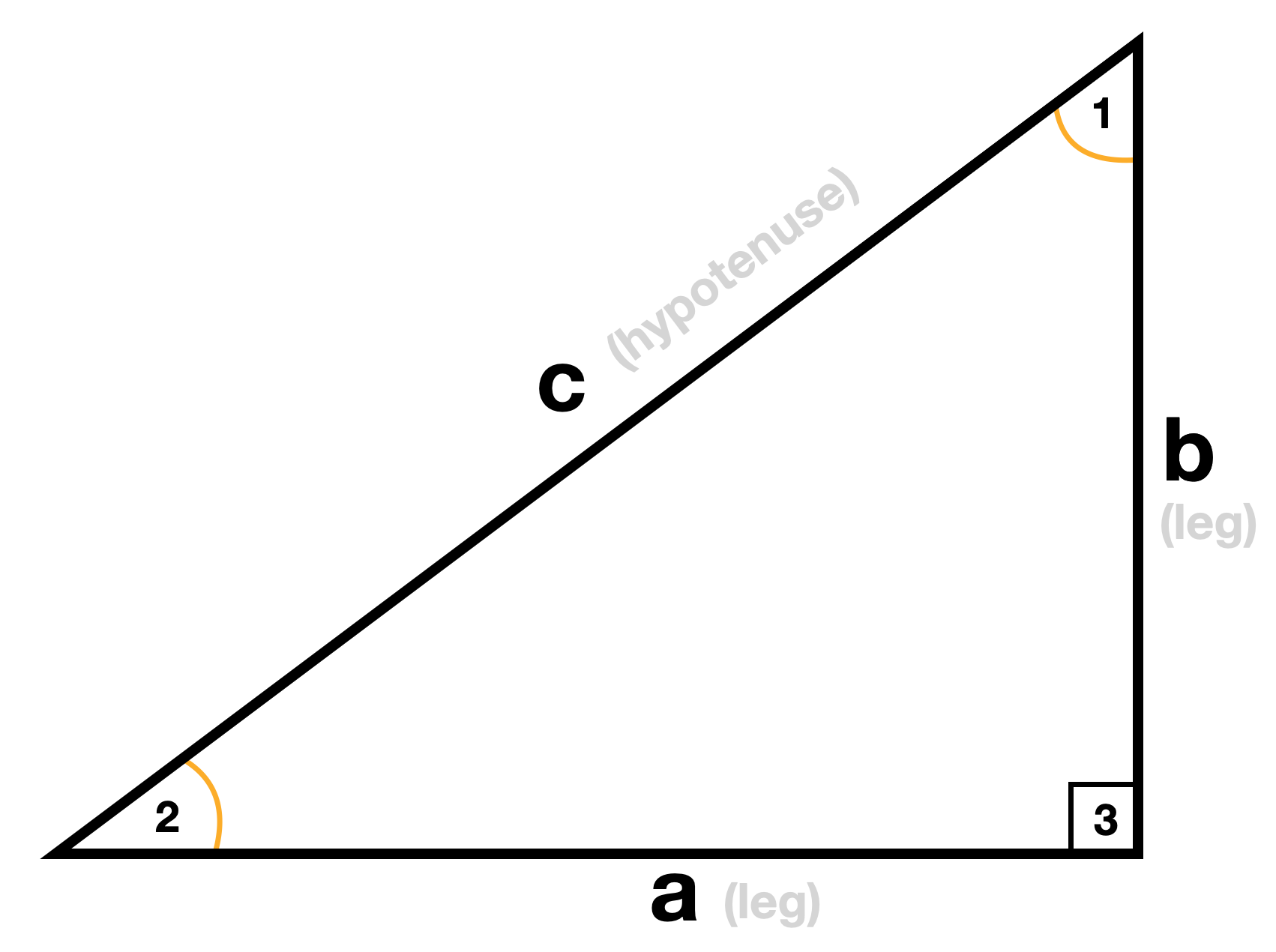
Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangle A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other Furthermore, how do you solve a 30 60 90 Triangle calculator?Calculator Use A right triangle is a special case of a triangle where 1 angle is equal to 90 degrees In the case of a right triangle a 2 b 2 = c 2 This formula is known as the Pythagorean Theorem In our calculations for a right triangle we only consider 2




Special Right Triangle Wikipedia




30 60 90 Triangle Theorem Ratio Formula Video
30° 60° Triangle Calculator Long Side Short Side Hypotenuse Area Perimeter Note Fill in any item and get the result of other items by clicking "Calculate" button 30 ̊ 60 ̊ Rad π/6 π/3 Sine 05 Cosine 05 Tangent Cotangent30°60°90° triangle The 30°60°90° refers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is knownLong side: Short side: Hypotenuse: Area: Perimeter: App description 30 60 90 triangle calculation formula Area = 05 * Long side * Short side;



How To Work With 30 60 90 Degree Triangles Education Is Around




Special Right Triangles Fully Explained W 19 Examples
Use our 30 60 90 right triangle calculator to solve the edge lengths, altitude, area, perimeter, and inradius of a triangle Side opposite the 90° angle 2x All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle in radians, it translates to the following In any triangle, you see the following A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middle



13 3 2 The 30 60 90 Triangle Graphing Calculator By Mathlab User Manual



Solve A 30 60 90 Triangle With Gradea
The triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 Here, a right triangle means being any triangle that contains a 90° angle A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°Enter 1 out of 3 to solve for the other 2 missing sides Special right triangle 30 60 90 is one of the most popular right triangles The 30 60 90 right triangle is a special case triangle with angles measuring 30 60 and 90 degrees If you want to read more about that special shape check our calculator dedicated to the 30 60 90 triangleThe 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
Solve problems involving right triangles Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 4 inches and 4√3 inches Step 3 Calculate the third side Answer The length of the hypotenuse is 8 inches You can also recognize a triangle by the anglesA triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio o



13 3 2 The 30 60 90 Triangle Graphing Calculator By Mathlab User Manual
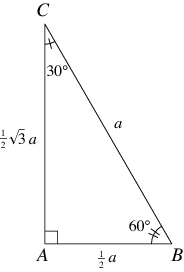



30 60 90 Triangle From Wolfram Mathworld
A 30 60 90 triangle is a special right triangle that has interior angles measuring 30°, 60°, and 90°A triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sidesThe Triangle Graphing Calculator by MathlabUser Manual 1332 The 30°60°90° Triangle In a 30°60°90° right triangle, the length of the hypotenuse is twice the length of the shorter leg (side opposite the 30° angle) and the length of the longer leg (side opposite the 60° angle) is sqrt (3) times the length of the




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
The graphics posted above show the 3 cases of a 30 60 90 triangle If you know just 1 side of the triangle, the other 2 sides can be easily calculated For example, if you only know the short side (figure5), the medium side is found by multiplying this by the square root of 3 (about 1732) and the hypotenuse is calculated by multiplying the short side by 2 About Triangle A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric featuresIt will even tell you if more than 1 triangle can be created
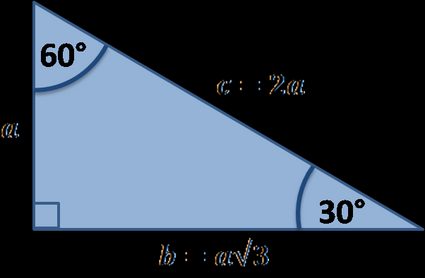



30 60 90 Triangle Calculator Formula Rules
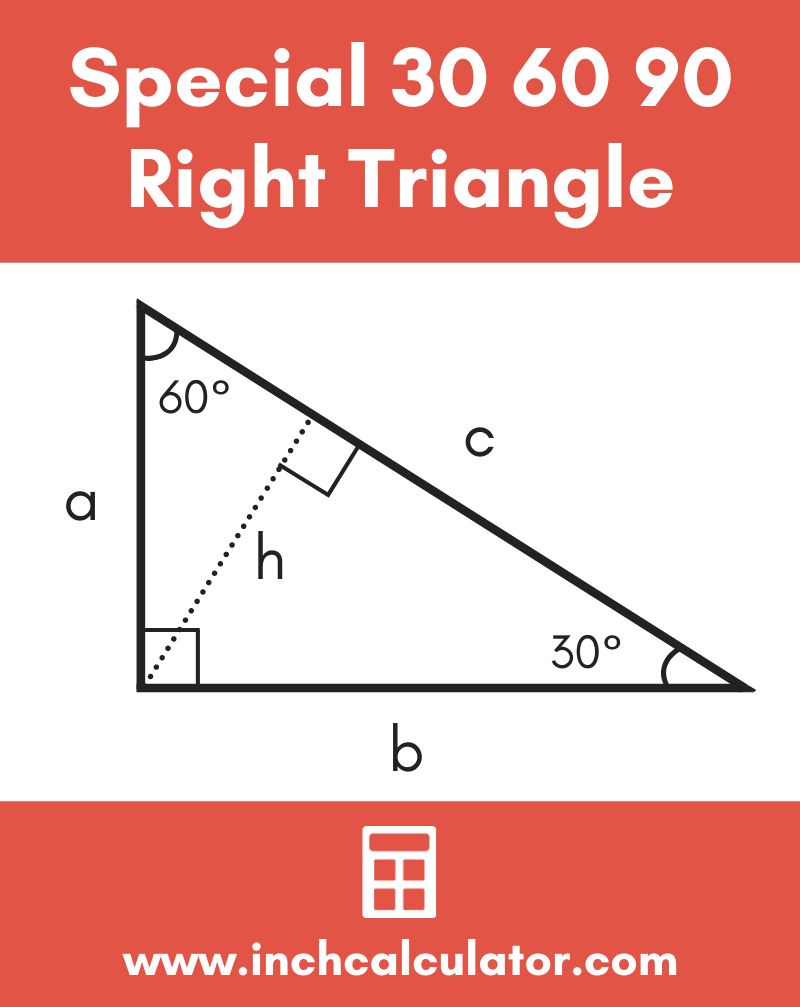



30 60 90 Special Right Triangle Calculator Inch Calculator
A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, andA 30 60 90 right triangle literally pronounced thirty sixty ninety is a special type of right triangle where the three angles measure 30 degrees 60 degrees and 90 degrees If you want to read more about that special shape check our calculator dedicated to the 30 60 90 triangle It has been illustrated in the diagram shown below 30 60 90 triangle sides calculator If you just know the length of one "leg" of a 45 45 90 triangle (figure 8), multiply it by the square root of 2 (about 1414) to obtain the hypotenuse length Clicking "RESET" clears all of the boxes Triangles are classified as "special right triangles" Calculate the cyclist's average speed in mph




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




30 60 90 45 45 90 Special Right Triangles Youtube
Special right triangle 30° 60° 90° is one of the most popular right triangles Its properties are so special because it's half of the equilateral triangle If you want to read more about that special shape, check our calculator dedicated to the 30° 60° 90° triangleThe area of a triangle equals 1/2base * height Use the short leg as the base and the long leg as the height Use the short leg as the base and the long leg as the height A thirty, sixty, ninety, triangle creates the following ratio between the angles and side lengthA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊ Formulas of triangle with angle 30̊ 60̊ 90̊ • perimeter = long side short side hypotenuse;
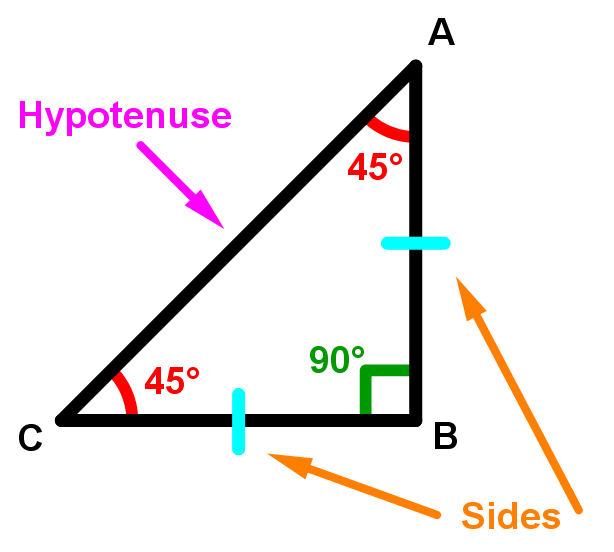



How To Use The Special Right Triangle 45 45 90 Studypug




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
From this page you will also find more information of 30 60 90 calculator, which is many times referred as special right triangle What is a 30 60 90 triangle?Triangle 30 60 90 Calculator This is a special right triangle having 30, 60, and 90 angles from all sides In order to perform specific calculations regarding this type of triangle, you can take the support of different branches of mathematics including trigonometry Memorizing and understanding your triangles will also allow you to solve many trigonometry problems without the need for a calculator or needing to approximate your answers in decimal form A triangle has fairly simple sines, cosines, and tangents for each angle (and these measurements will always be consistent)




30 60 90 Triangle Rules Calculator Formula The Free Calculator



30 60 90 Triangle Rules Calculator Formula The Free Calculator
A right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads) The sides of a right triangle lie in the ratio 1√32Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units inSpecial Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangle
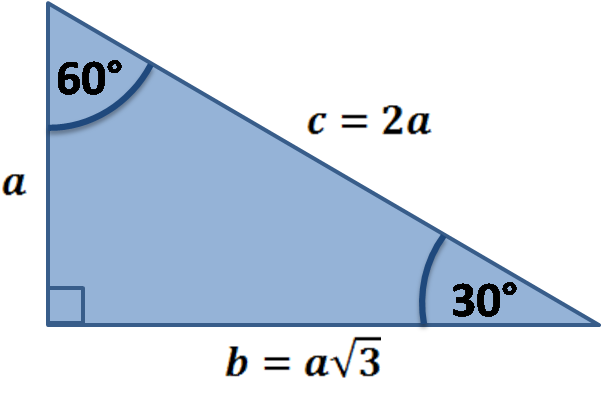



30 60 90 Triangle Calculator Online Discount Shop For Electronics Apparel Toys Books Games Computers Shoes Jewelry Watches Baby Products Sports Outdoors Office Products Bed Bath Furniture Tools Hardware




The Complete Guide To The 30 60 90 Triangle
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the side oppositeCircumference = long side short side hypotenuse;30 60 90 degree right triangle calculator Category Geometric Help edit Enter a number and click "calculate"!



1




How To Find The Area Of A Right Triangle Basic Geometry
Thanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 in because c = 2b√3/3 = 2a ~ 127 inLong edge = hypotenuseComplete the following table Use the 30° 60° 90° and 45° 45° 90° triangles Do not use a calculator sin θ cos θ tan θ 45° cot θ sec θ csc θ (Simplify your answers Type exact answers, using radicals as needed) Question Complete the following table Use the 30° 60° 90° and 45° 45° 90° triangles



Special Right Triangle 30 60 45 45 37 53 Elearning
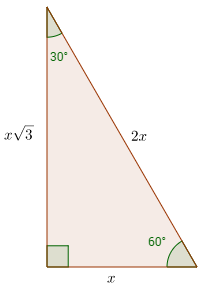



Special Right Triangles Video Lessons Examples And Solutions



30 60 90 And 45 45 90 Triangle Calculator
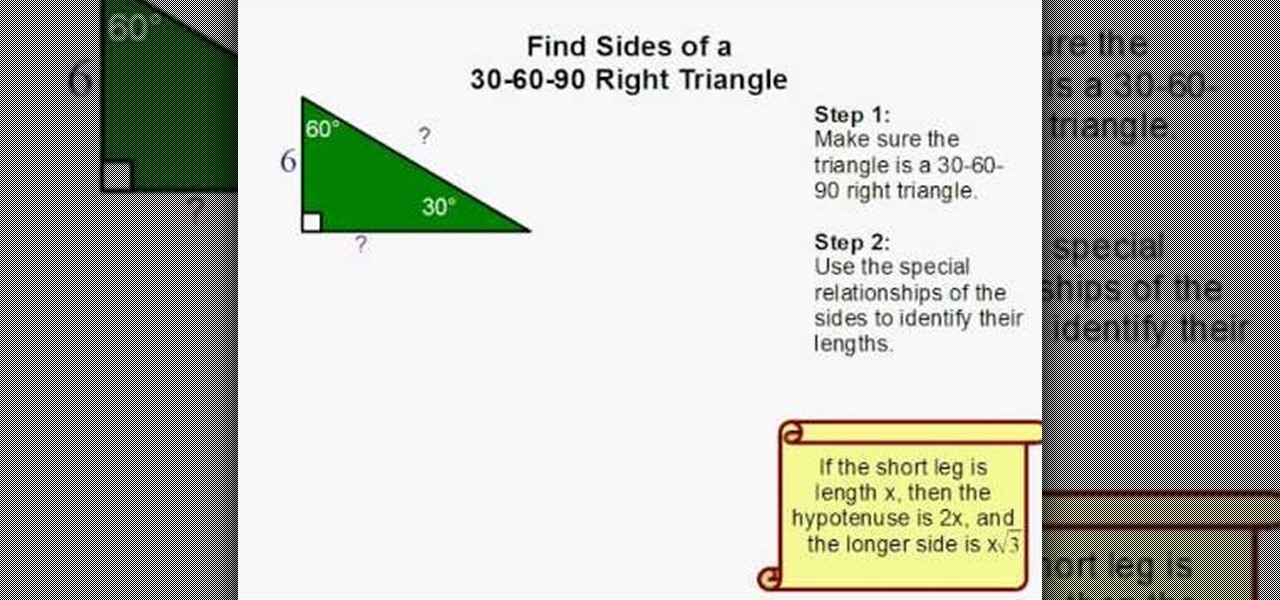



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto
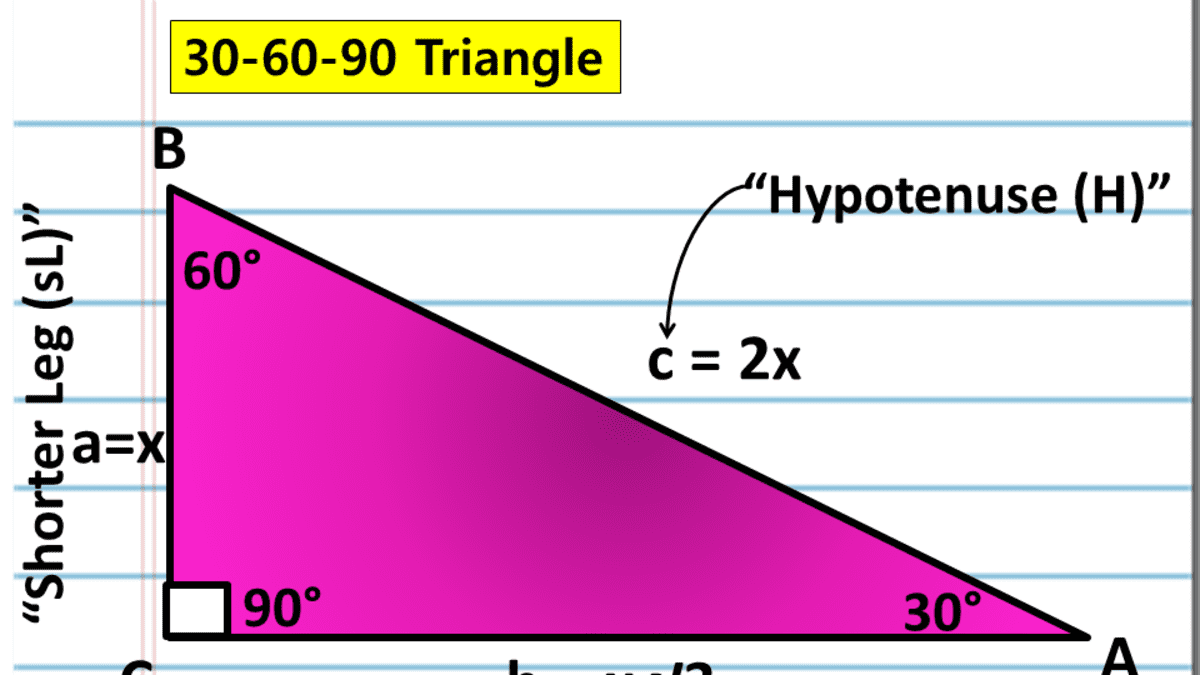



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Calculator Formula Rules
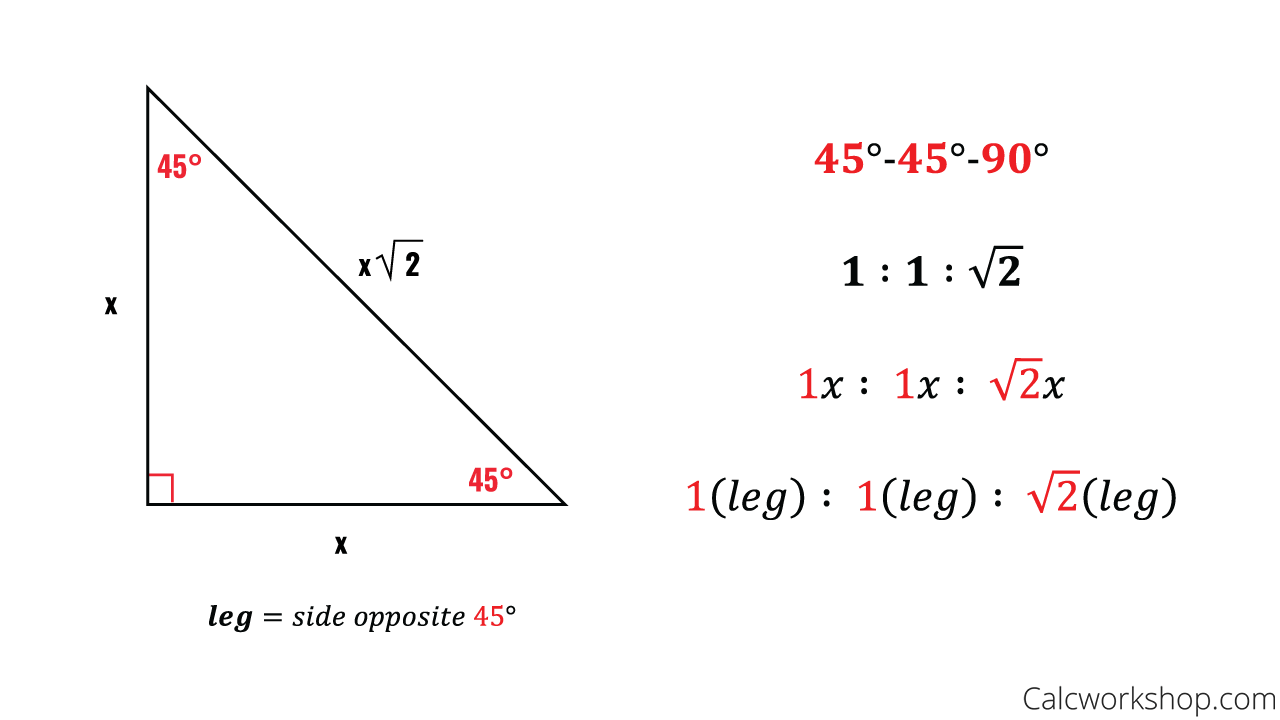



Special Right Triangles Fully Explained W 19 Examples



The Easy Guide To The 30 60 90 Triangle



30 60 90 Special Right Triangle Calculator Inch Calculator




Special Right Triangles Review Article Khan Academy



Right Triangles Calculator



30 60 90 Triangle From Wolfram Mathworld



Special Right Triangles Sss a Examples Included




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 And 45 45 90 Triangle Calculator



Area Of A Triangle



30 60 90 And 45 45 90 Triangle Calculator



Right Triangles Gmat Free




30 60 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Triangle Calculator Formula Rules




File 30 60 90 Triangle 2 Svg Wikimedia Commons



Right Triangle Calculator Pi Day



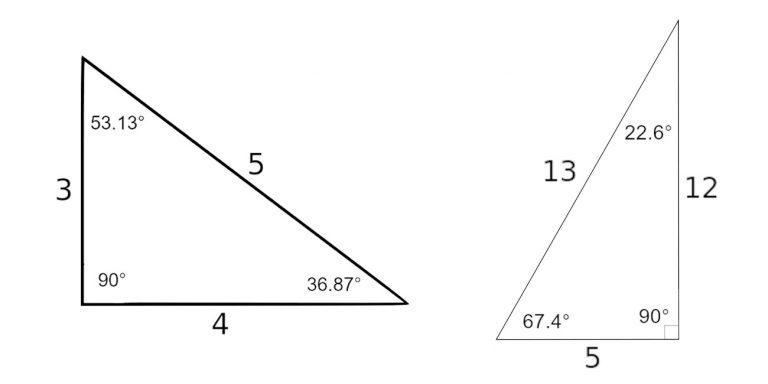
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




30 60 90 Triangle Sides Examples Angles Full Lesson
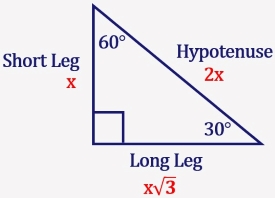



Special Right Triangle 30 60 90 Mathondemand Com
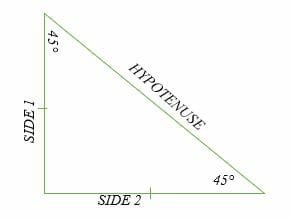



45 45 90 Triangle Explanation Examples




30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangles Intro Part 1 Video Khan Academy




Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




30 60 90 Triangle Calculator Purecalculators
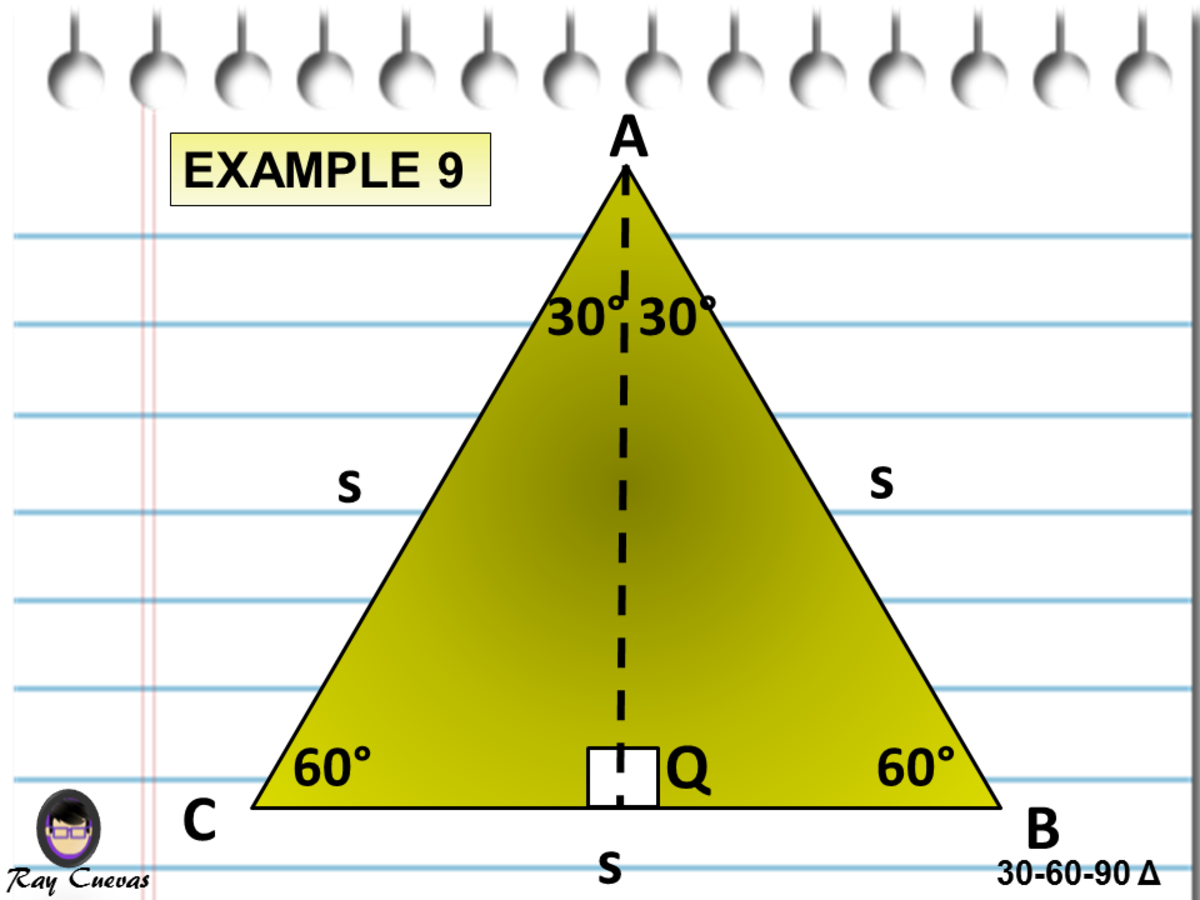



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



1




45 45 90 Triangle Calculator Formula Rules




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 And 45 45 90 Triangle Calculator



3
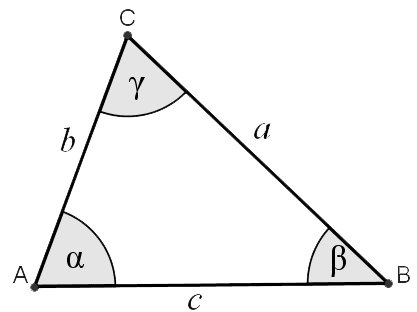



Triangle Calculator




Triangle Calculator Square Footage Area




30 60 90 Triangle Formulas Rules And Sides Science Trends



30 60 90 Triangle Rules




Solved U9 L4 Special Right Triangles Practice An Altitude H Chegg Com



Right Triangles Gmat Free




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Ratio Formula Video




Velocity
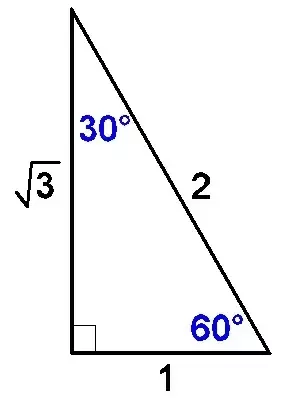



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic




5 30 60 90 Triangles Geometry15a
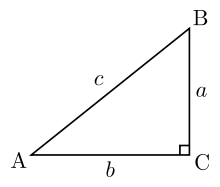



30 60 90 Right Triangle Calculator
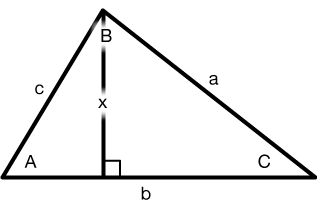



Non Right Triangle Trig




A Quick Guide To The 30 60 90 Degree Triangle Dummies
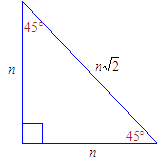



Special Triangles Isosceles And 30 60 90 Calculator
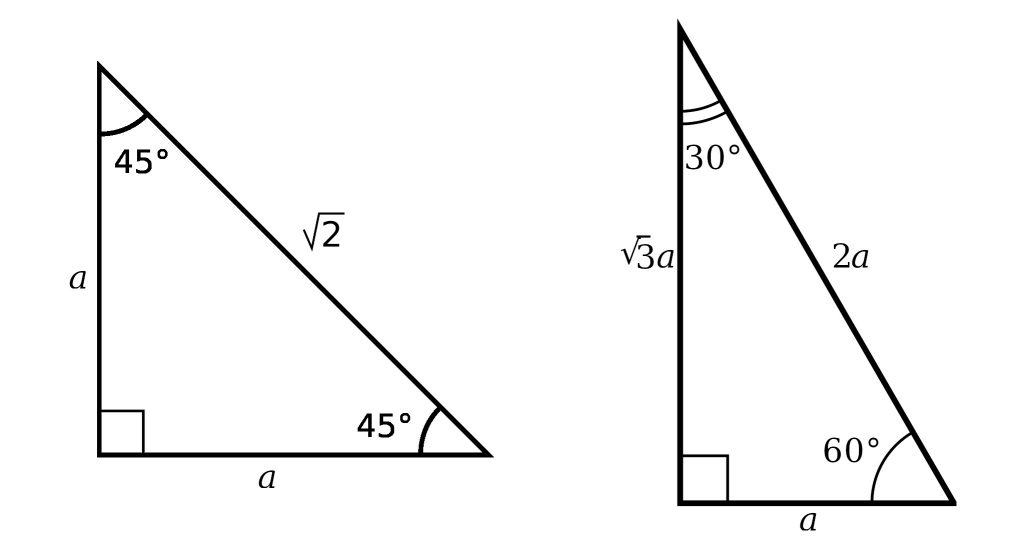



Special Right Triangles Sss a Examples Included




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Special Right Triangles Youtube
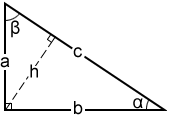



Right Triangle Calculator




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
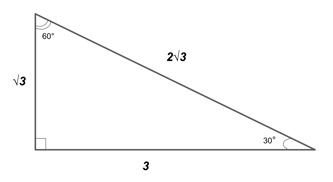



The Easy Guide To The 30 60 90 Triangle
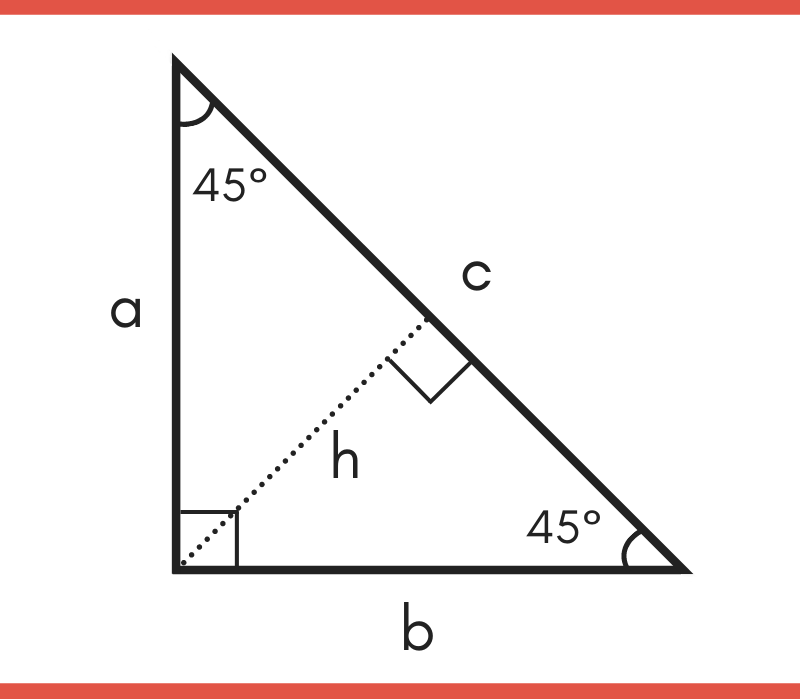



45 45 90 Special Right Triangle Calculator Inch Calculator
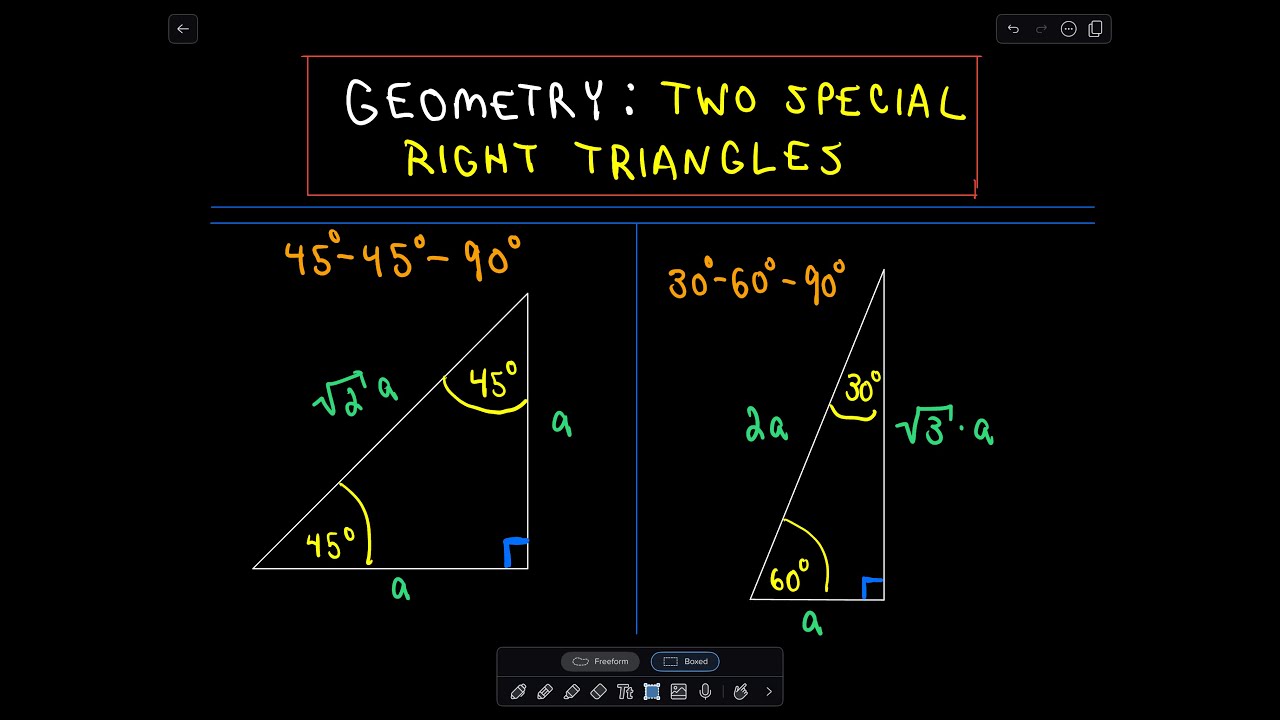



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube



Right Triangle Calculator And Solver




30 60 90 Triangle Theorem Ratio Formula Video
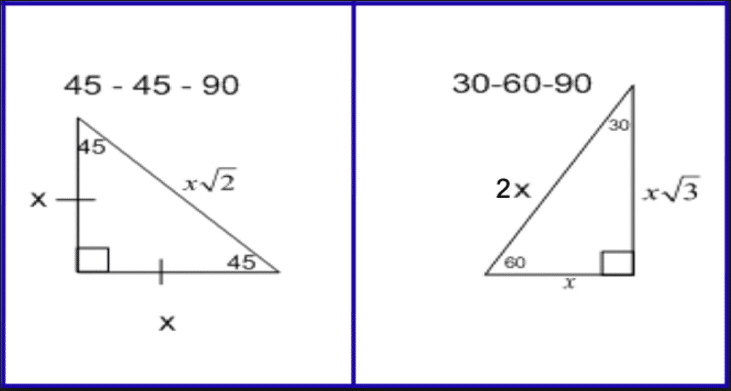



Special Right Triangles Complete Reference Guide The Education
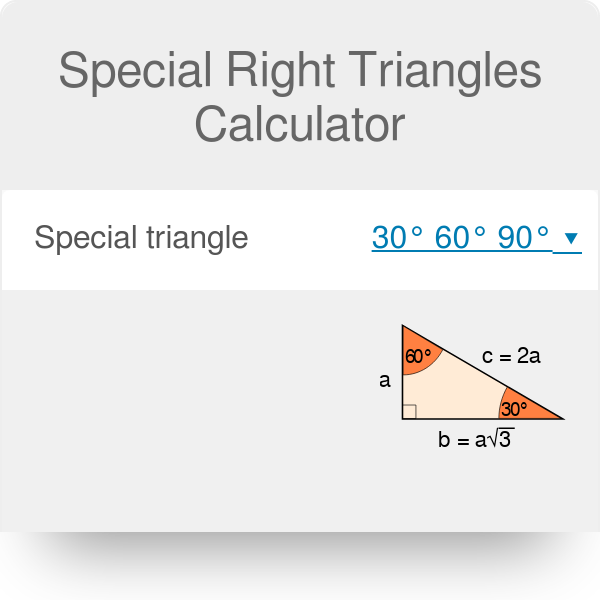



Special Right Triangles Calculator Formula Rules




30 60 90 Right Triangles Solutions Examples Videos




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




30 60 90 Triangle Calculator Formula Rules



Triangle 30 60 Calculator Endmemo
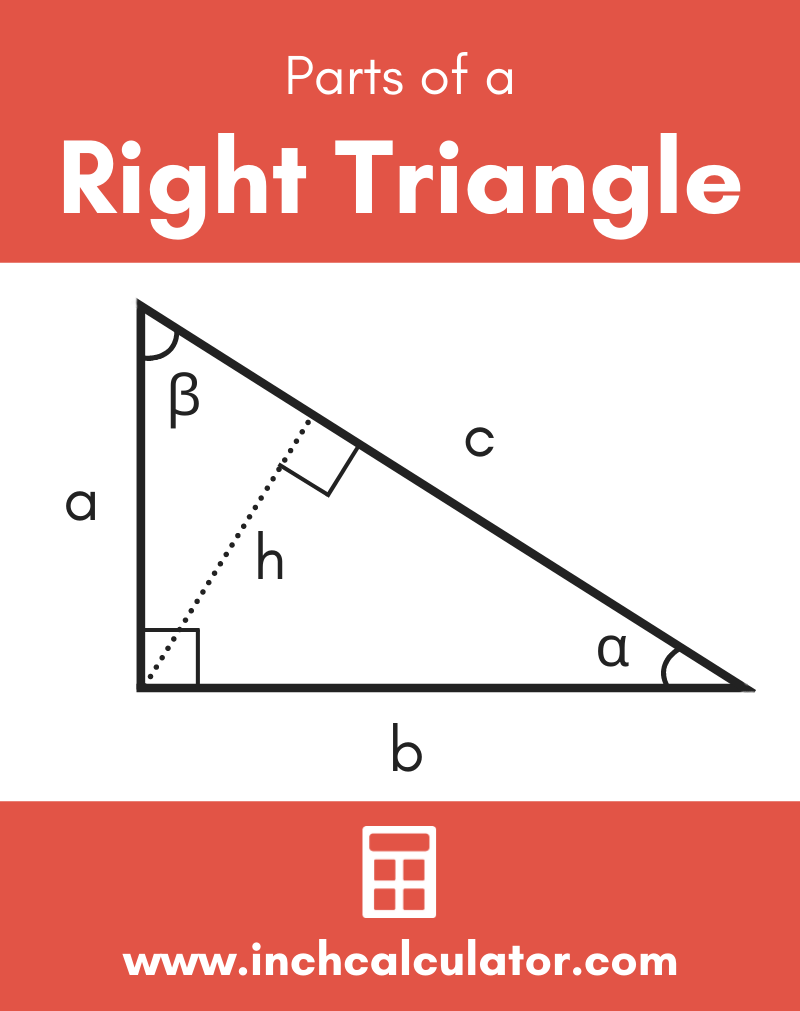



Right Triangle Calculator Solve Any Edge Or Angle Inch Calculator




30 60 90 Right Triangles Free Math Help
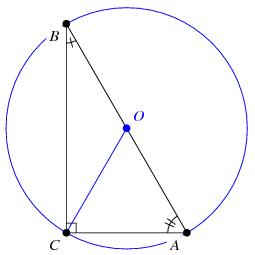



30 60 90 Triangle From Wolfram Mathworld



The Easy Guide To The 30 60 90 Triangle
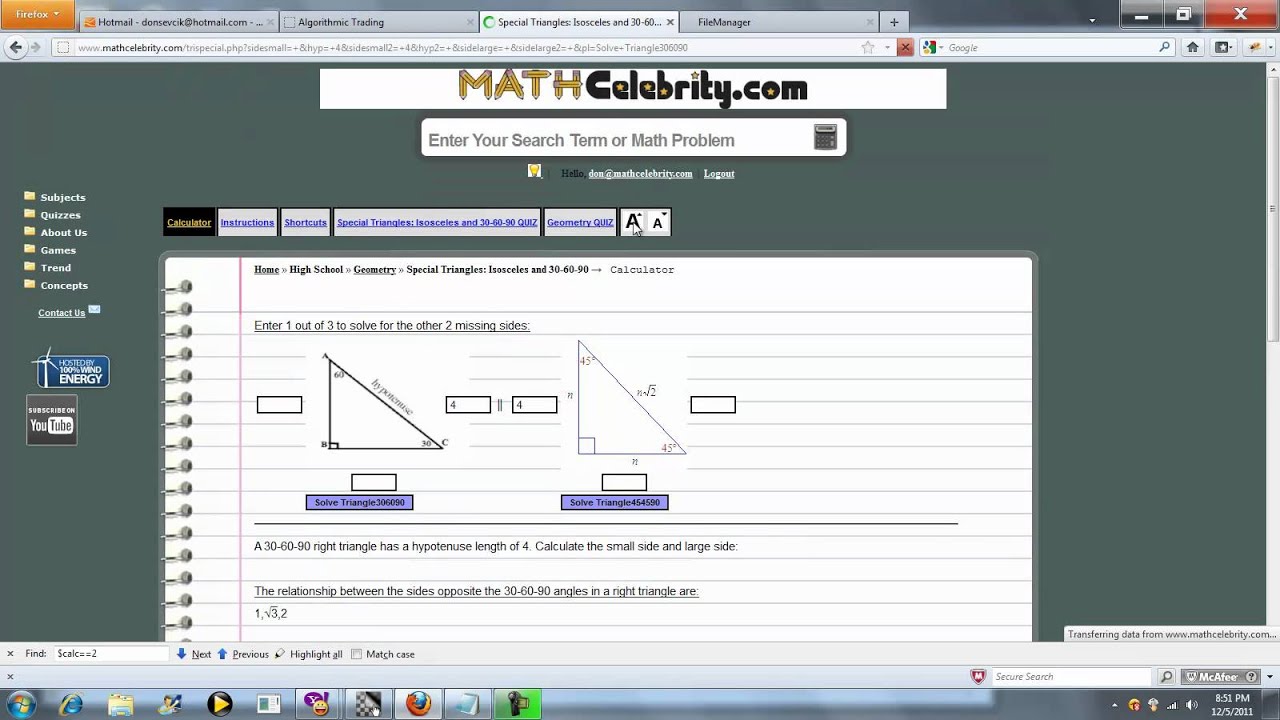



Special Triangles Isosceles And 30 60 90 Calculator




Learn About The 30 60 90 Triangle Caddell Prep Online




Solved Lesson 4activity Printables Tes Htm Part Chegg Com




The Complete Guide To The 30 60 90 Triangle
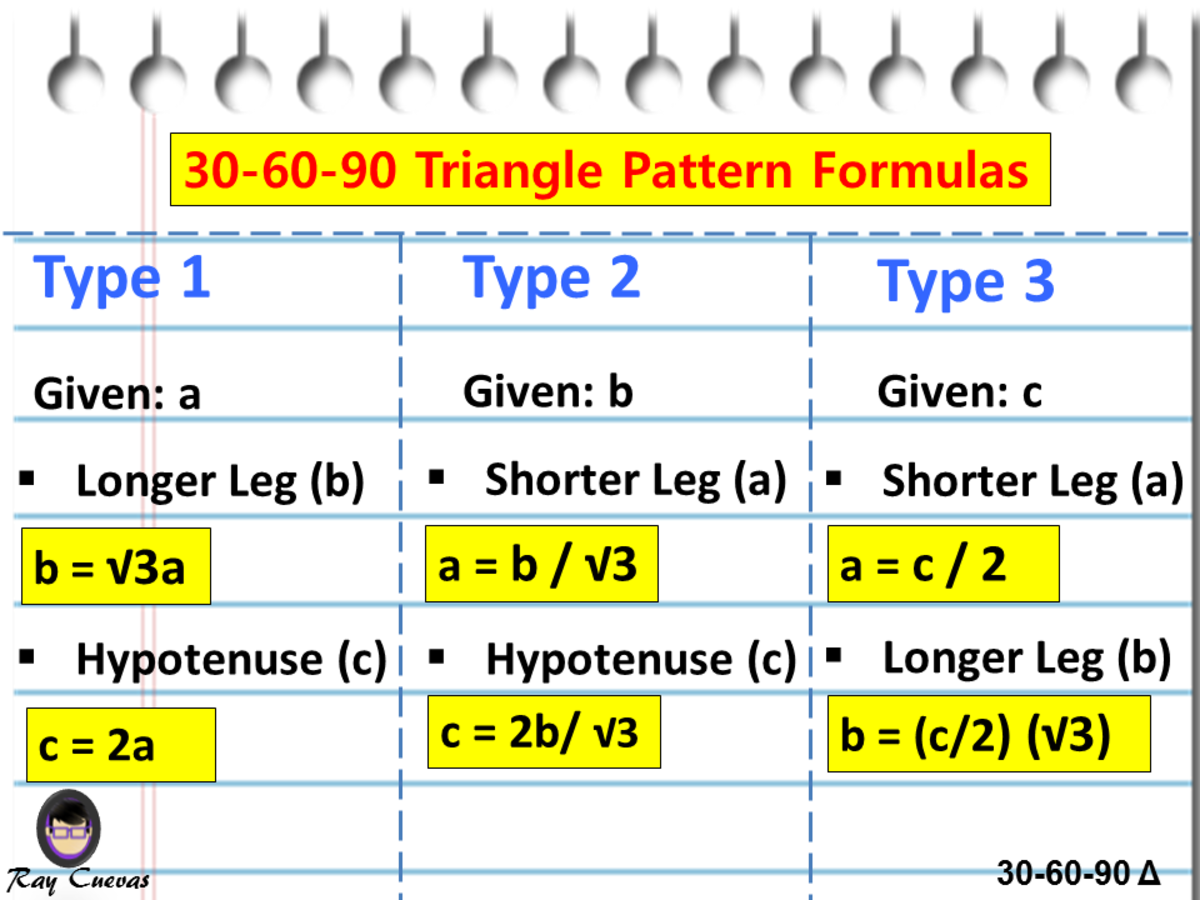



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Calculator Formula Rules
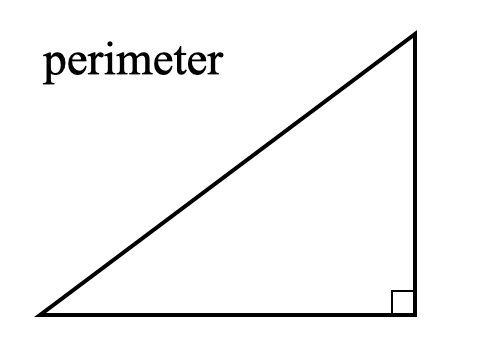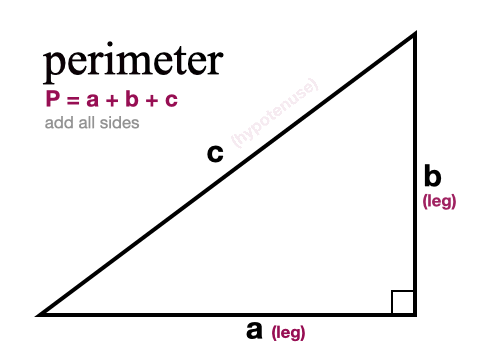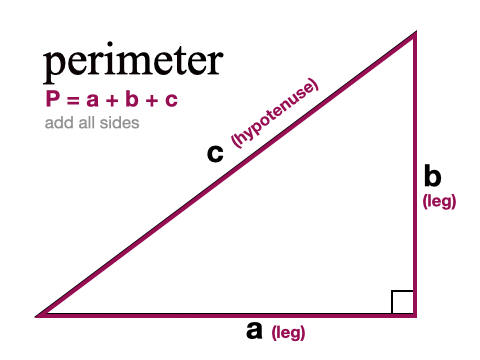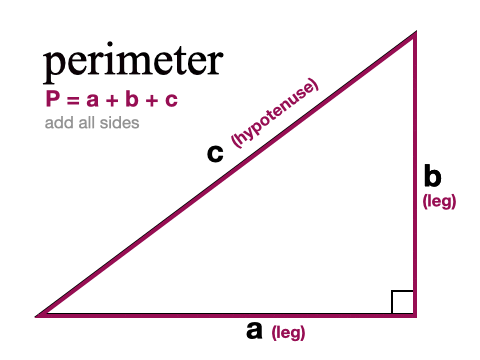



Right Triangle Calculator Pi Day



0 件のコメント:
コメントを投稿