Using what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected itemB) 95°, 30°, 55° c) °, 45°, 46° d) 90°, 60°, 30° Solution An obtuseangled triangle has one of the vertex angles as an obtuse angle (> 90°) Among the given options, option (b) satisfies the condition Therefore, option b ie 95°, 30°, 55° forms an obtuse triangleA triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 What is the formula for a

30 60 90 Triangles
30 60 and 90 triangle formula radical
30 60 and 90 triangle formula radical- A right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√ (3/2) This means that the hypotenuse is twice as long as the shorter leg and the longer leg is the square root ofArea of a Triangle The formula to calculate the area of a triangle is = (1/2) × base × height In a rightangled triangle, the height is the perpendicular of the triangle Thus, the formula to calculate the area of a rightangle triangle is = (1/2) × base × perpendicular




30 60 90 Triangle Theorem Ratio Formula Video
The two legs of a triangle are always equal The hypotenuse of the triangle is always opposite the right angle There are two formulas for the lengths of the sides of a triangle Then, what is the 30 60 90 triangle formula?Need more Geometry help? About Triangle A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric features
If you want to know what is the hypotenuse of a right triangle, how to find it and what is the hypotenuse of a triangle formula, you'll find the answer below, with a simple example to clear things up Don't wait any longer, give this hypotenuse calculator a try!A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, andThe reason these triangles are considered special is because of the ratios of their sides they are always the same!
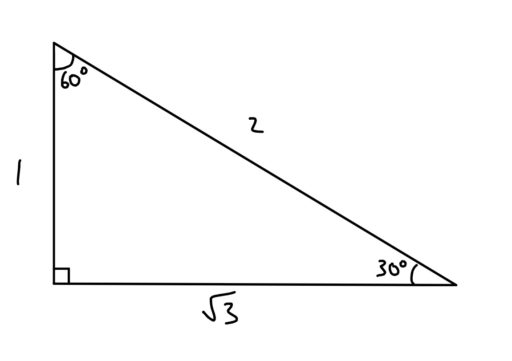
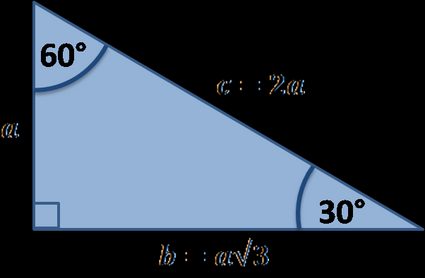
Right triangles are one particular group of triangles and one specific kind of right triangle is a right triangle As the name suggests,A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the same tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees) Since the right angle is always the largest angle, the hypotenuse is always the longest side using property 2 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=c




A Quick Guide To The 30 60 90 Degree Triangle Dummies



Tarantamath Licensed For Non Commercial Use Only Razan 10 3
Triangle 30 60 90 Calculator This is a special right triangle having 30, 60, and 90 angles from all sides In order to perform specific calculations regarding this type of triangle, you can take the support of different branches of mathematics including trigonometry Triangle 30 All you have to do is recall the triangles formula which was shared ealier which is x2xx\sqrt3 and apply it From our formula, we can find the value of our two other sides just by inputing the given value into the equation Where x is equals 5, the hypotenuse (2x) becomes 2 \times 5 = 10, while the adjacent side becomes x\sqrt {3 The two special right triangles are right triangles with interior angles measuring 30 60 90 and 45 45 90 What is the 45 45 90 triangle rule?



The Easy Guide To The 30 60 90 Triangle
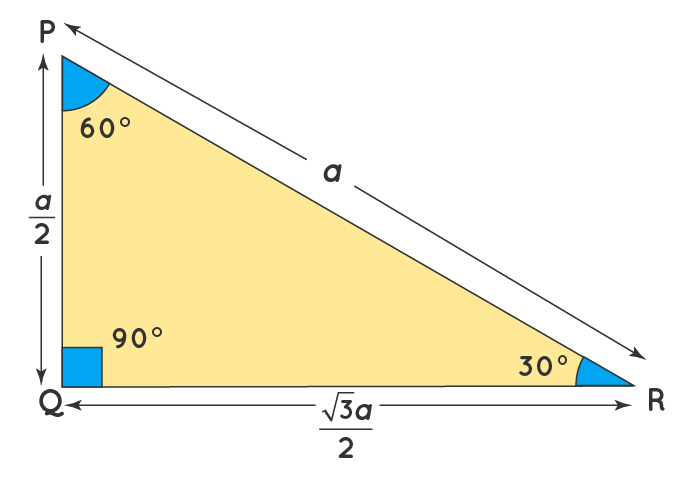



30 60 90 Triangle Definition Theorem Formula Examples
• area = 05 *Special Triangles The Triangle If you have one side, you can use these formulas (and maybe a little algebra) to get the others The Triangle If you have one side, you can use these formulas (and maybe a little algebra) to get the others A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Calculator Formula Rules
Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles Perimeter of a triangle = a b c Area of a triangle = 1 2bh A r e a o f a t r i a n g l e = 1 2 b h Where, b is the base of the triangle h is the height of the triangle If only 2 sides and an internal angle is given then the remaining sides and angles can be calculated using the below formula a sinA = b sinB = c sinC a s i n A = b s i nThe triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X , turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at



30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangles Review Article Khan Academy
The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to useVisit https//wwwmathhelpcom/geometryhelpIn this video, we use the 45°45°90° and 30°60°90° triangle formulas to find the misIn any triangle, you see the following The shortest leg is across from the 30degree angle, the length of the hypotenuse is always double the length of the shortest leg, and you can find the length of the long leg by multiplying the short leg by the square root of 3
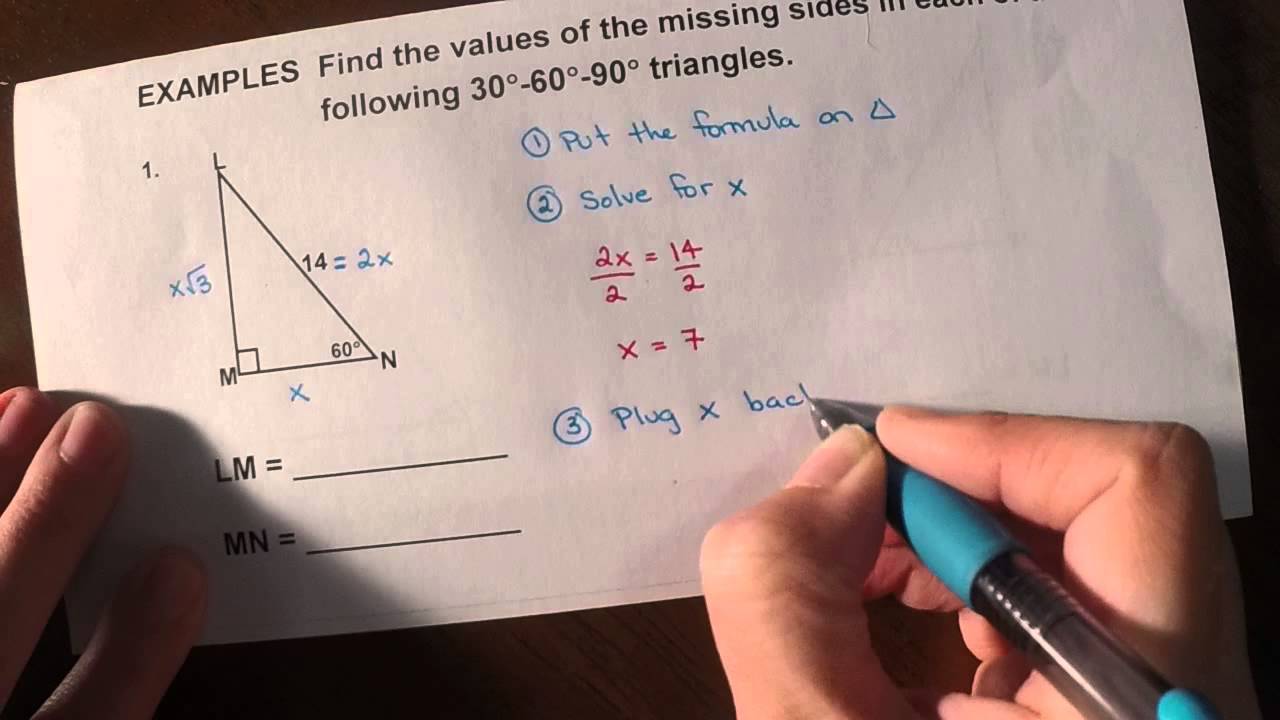



30 60 90 Triangles Youtube



1
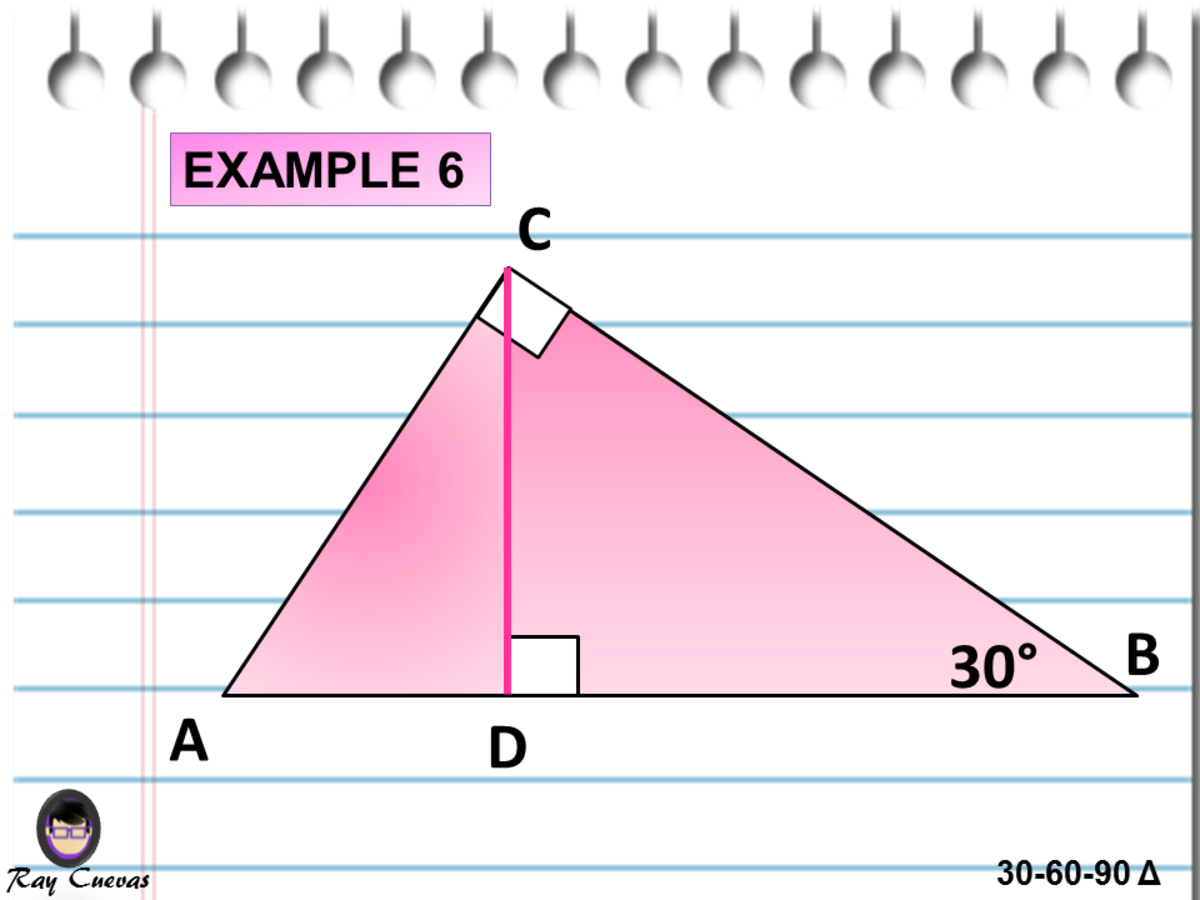
A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangleTriangle ABD therefore is a 30°60°90° triangle Now, since BD is equal to DC, then BD is half of BC This implies that BD is also half of AB, because AB is equal to BC That is, BD AB = 1 2 From the Pythagorean theorem, we can find the third side ADAnswer (1 of 3) A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a 30
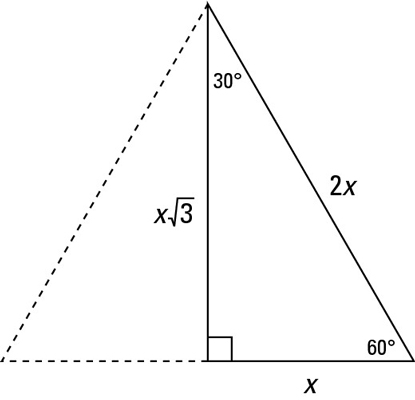



Identifying The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 230 60 90 triangle 45 45 90 triangle Area of a right triangleWhat is the formula for 30 60 90 Triangle?




30 60 90 Right Triangles Free Math Help




30 60 90 Triangle Explanation Examples
The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATThe property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle isA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊ Formulas of triangle with angle 30̊ 60̊ 90̊ • perimeter = long side short side hypotenuse;



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Appendix All The Formulas
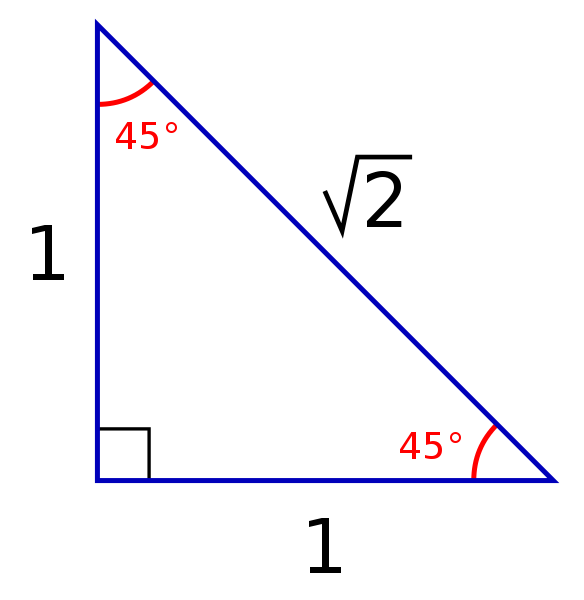
The 45 45Example We multiply the length of the leg which is 7 inches by √2 to get the length of the hypotenuse $$7\cdot \sqrt{2}\approx 99$$ In a 30°60° right triangle we can find the length of the leg that is opposite the 30° angle by using this formulaThe first concept of a triangle is the pattern of x, x√3,2x which Sal represents as a ratio of 1, √3, 2 Using the Pythagorean Theorem, (1)^2 (√3)^2 = (2)^2 or 1 3 = 4 This ratio will be true of every



1




30 60 90 Triangle Calculator Formula Rules
It turns out that in a triangle, you can find the measure of any of the three sides, simply bySpecial right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangle30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a



Isosceles Triangle




Determine The Missing Short Leg And Hypotenuse Of A 30 60 90 Triangle Youtube
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherThen ABD is a 30°–60°–90° triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progressionTo learn more about Triangles enrol in our full course now https//bitly/Triangles_DMIn this video, we will learn 000 triangle017 proof of 306



Special Right Triangle 30 60 45 45 37 53 Elearning



My College Options Triangles
See also Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangle




A Quick Guide To The 30 60 90 Degree Triangle Dummies



30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangles



30 60 90 Triangle Formulas Rules And Sides Science Trends



Solution I Dont Know How Do 30 60 90 Triangles That Already Have One Side And Also 45 45 90 Triangles And Sin 1 And All That Please Help




30 60 90 Triangle Definition Theorem Formula Examples
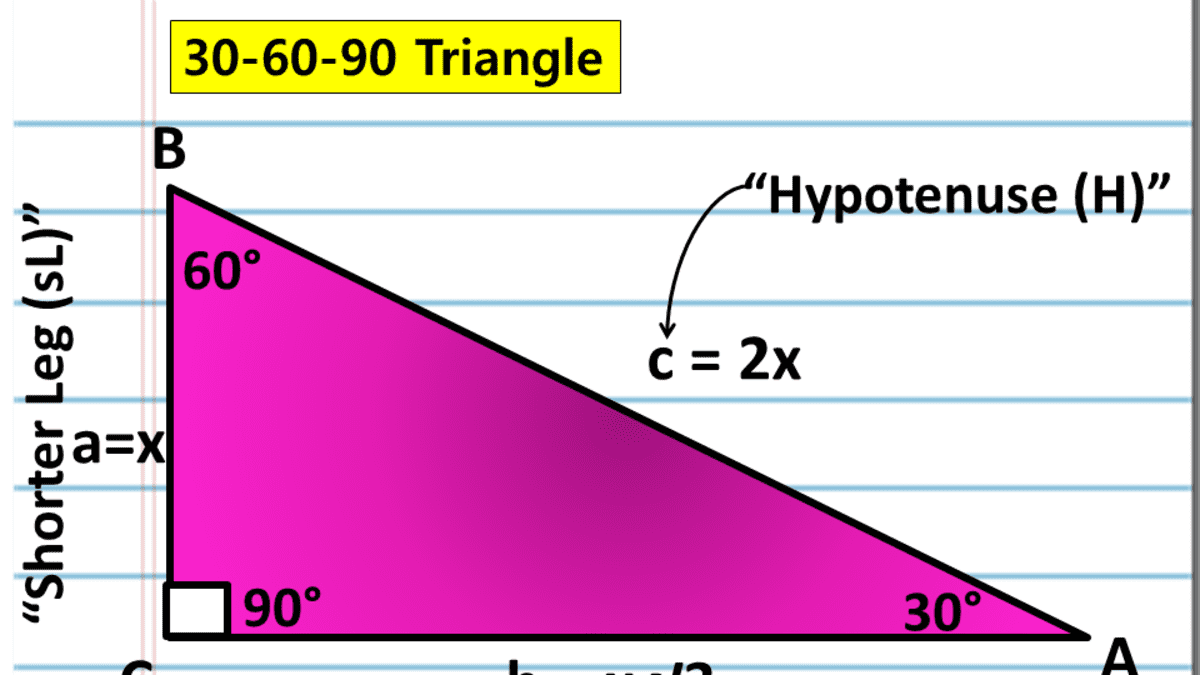



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



45 45 90 And 30 60 90 Triangles Zona Land Education




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math
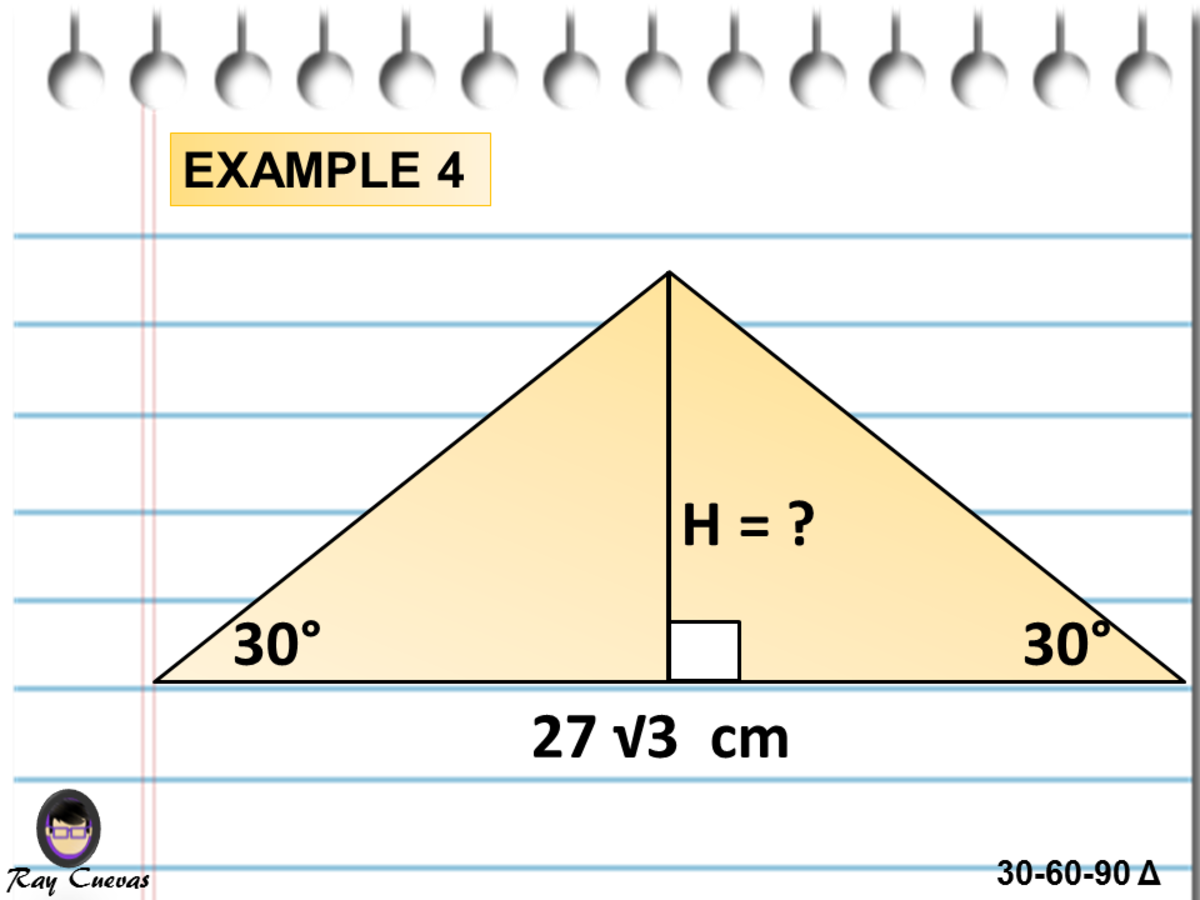



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Ratio Formula Video



The Easy Guide To The 30 60 90 Triangle
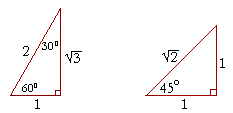



The 30 60 90 Triangle Topics In Trigonometry




Special Right Triangles Video Lessons Examples And Solutions
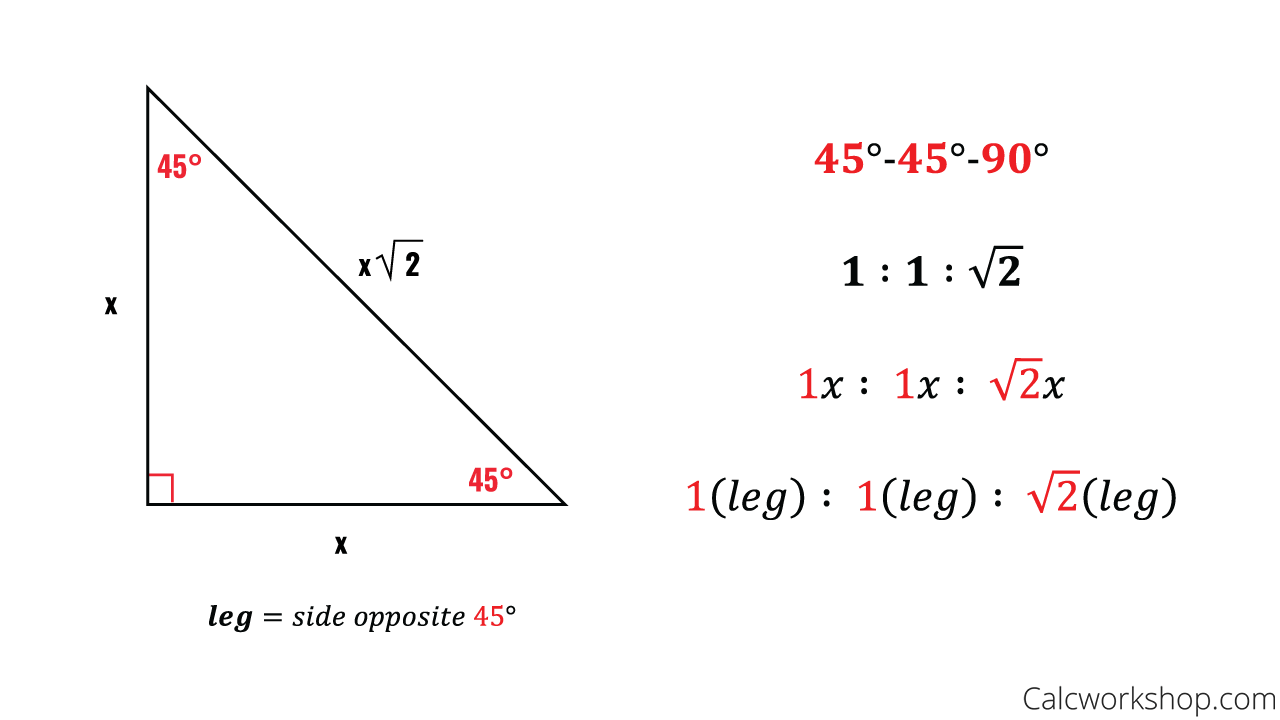



Special Right Triangles Fully Explained W 19 Examples
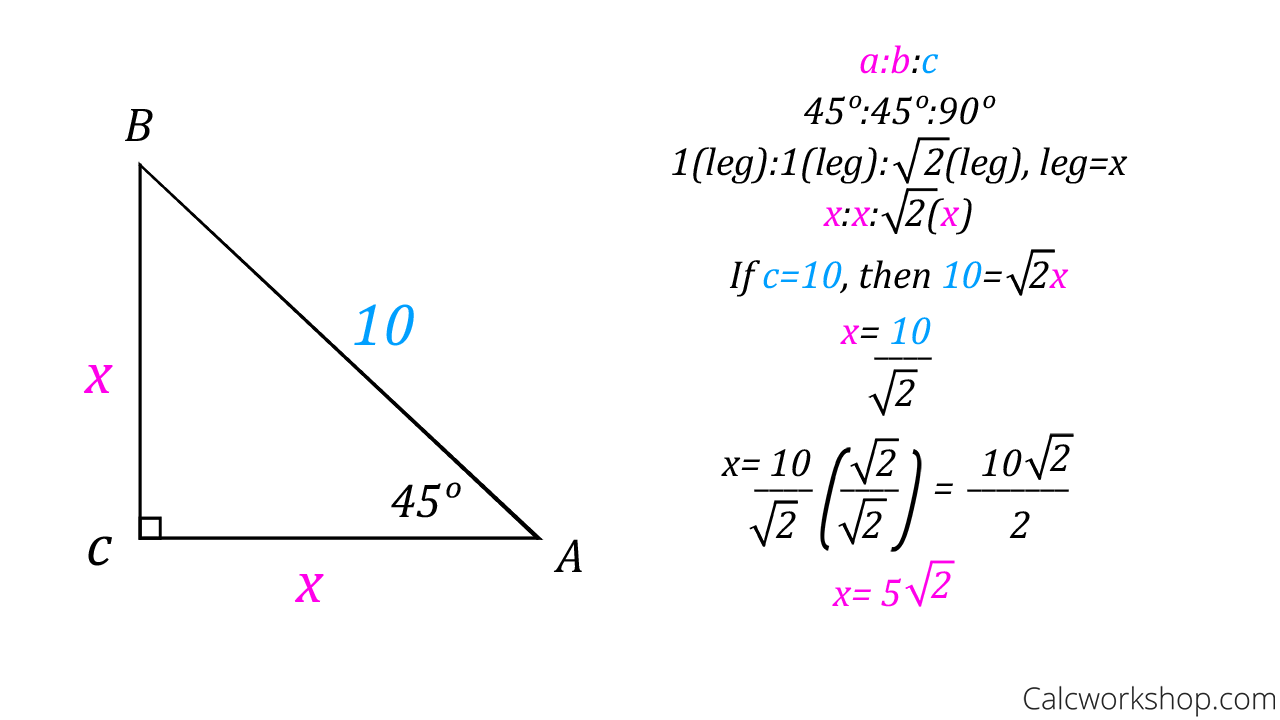



Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangles
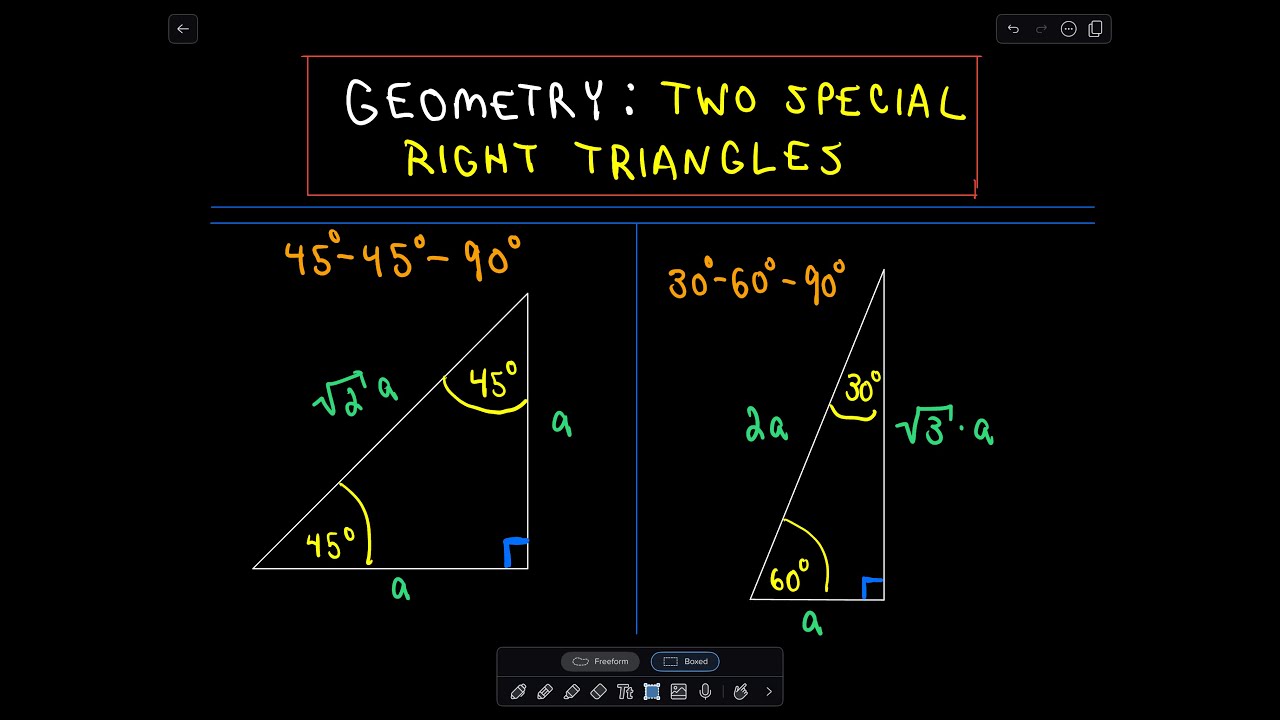



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video



Right Triangle Formulas Xgeometry



1
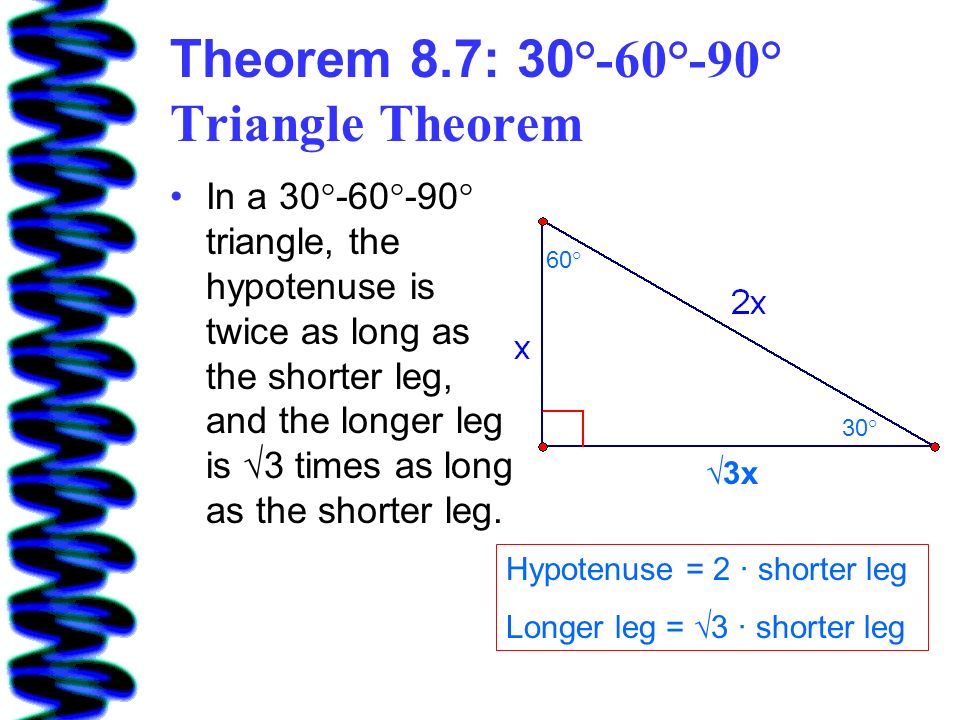



8 2 Special Right Triangles Ppt Video Online Download




Right Triangle Wikipedia




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Part 1 45 45 90 And 30 60 90 Youtube




30 60 90 Triangle Example Problem Video Khan Academy
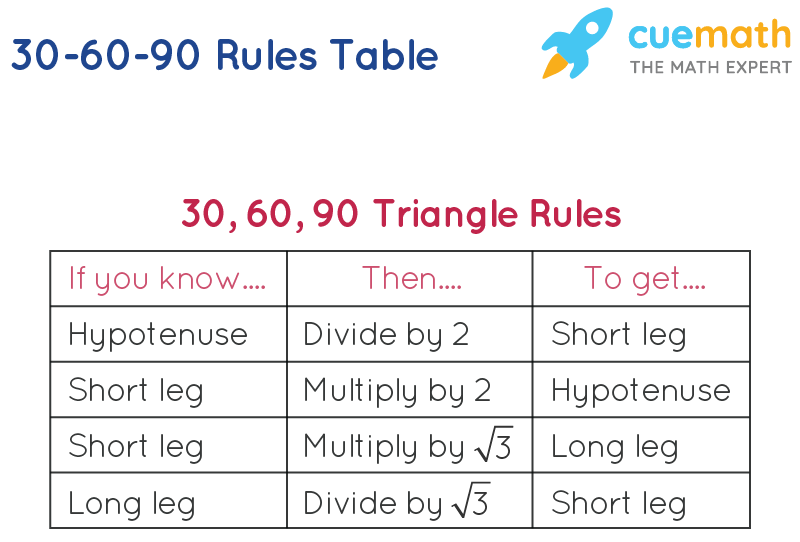



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
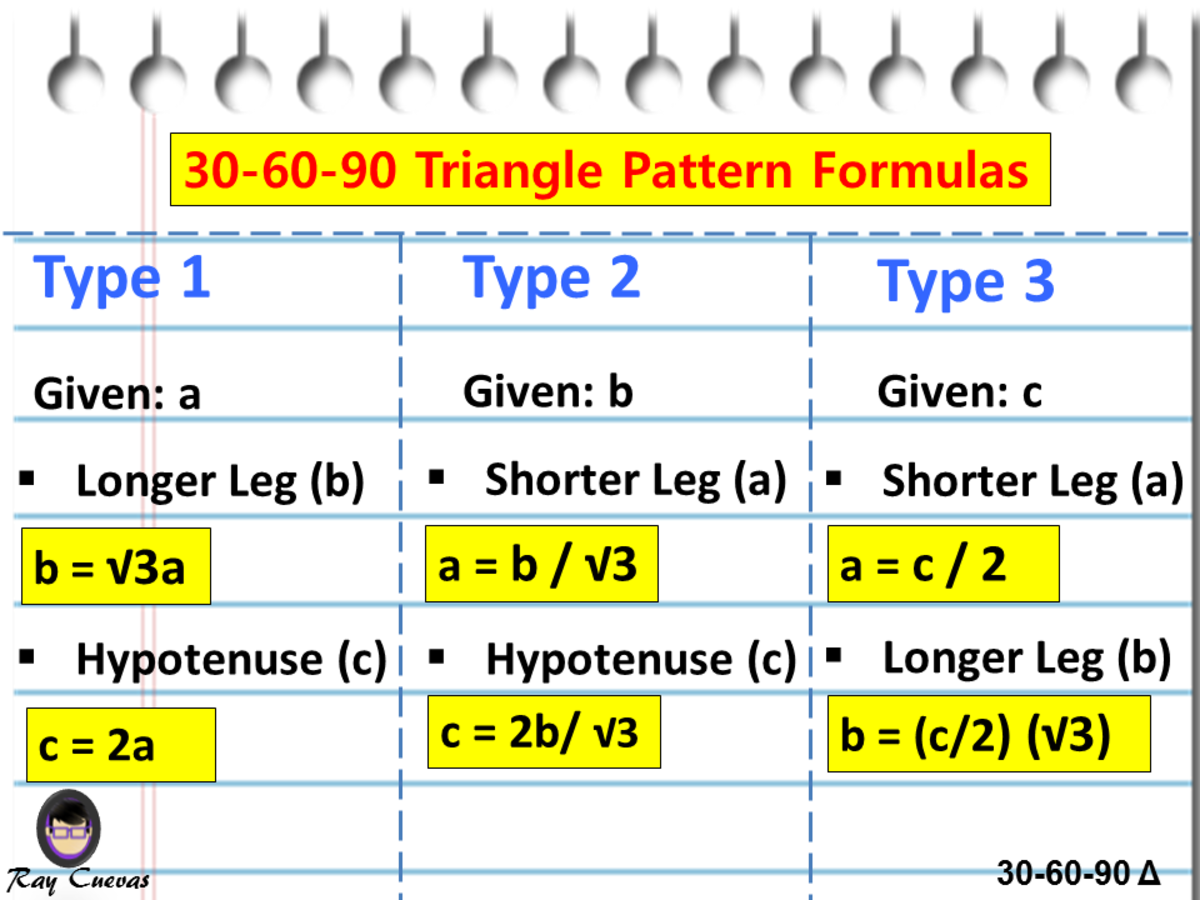



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Solution What If The Short Side Of A 30 60 90 Triangle Has A Radical




30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures
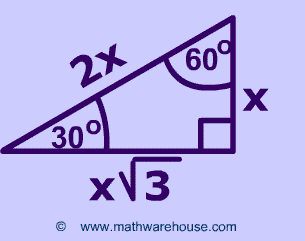



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
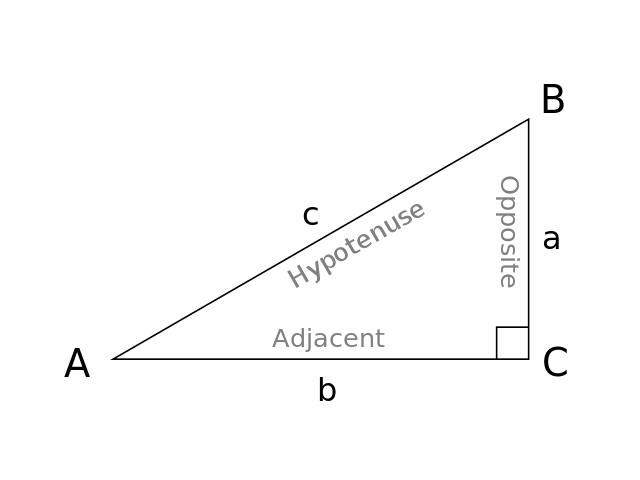



30 60 90 Triangle Formulas Rules And Sides Science Trends




Know How To Set Up Proportions For What Is The Ratio Chegg Com
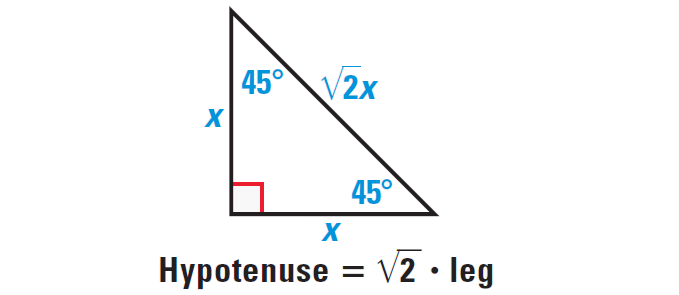



Special Right Triangles



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Right Triangle Side Ratios Expii




Special Right Triangle Wikipedia




The 30 60 90 Triangle Topics In Trigonometry




Special Right Triangles Review Article Khan Academy




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
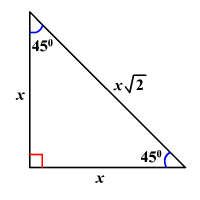



45 45 90 Triangles
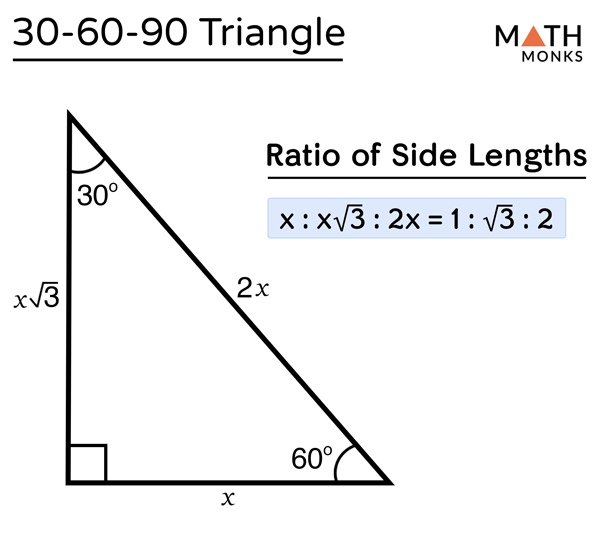



30 60 90 Triangle Definition Formulas Examples




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Inte Learning Mathematics Triangle Formula Math Formulas



File 30 60 90 Triangle 2 Svg Wikimedia Commons




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




The Complete Guide To The 30 60 90 Triangle




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
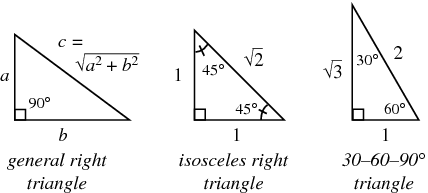



Right Triangle From Wolfram Mathworld



The Easy Guide To The 30 60 90 Triangle
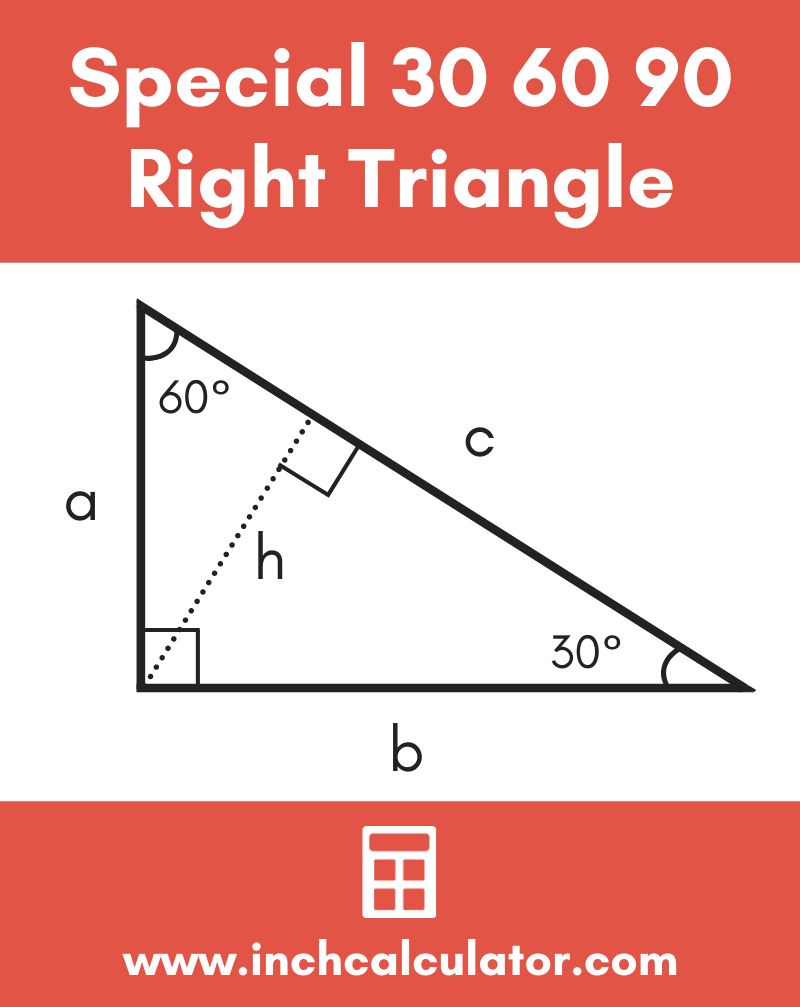



30 60 90 Special Right Triangle Calculator Inch Calculator




Foundation Class X Theorem Of 30 60 90 Triangle In Marathi Offered By Unacademy




How To Find The Area Of A Right Triangle Basic Geometry
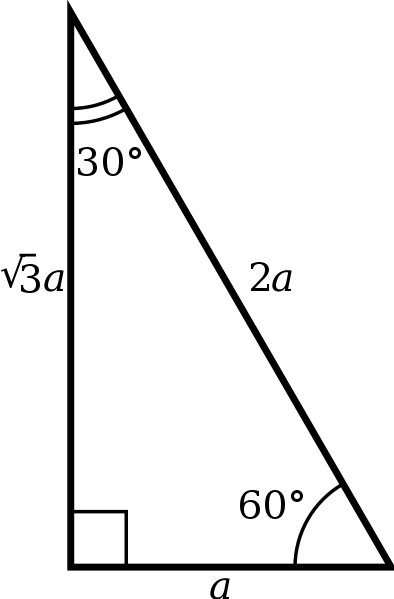



30 60 90 Triangle Formulas Rules And Sides Science Trends




Math Theorem Geometry Flashcards Quizlet




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Formulas Rules And Sides Science Trends
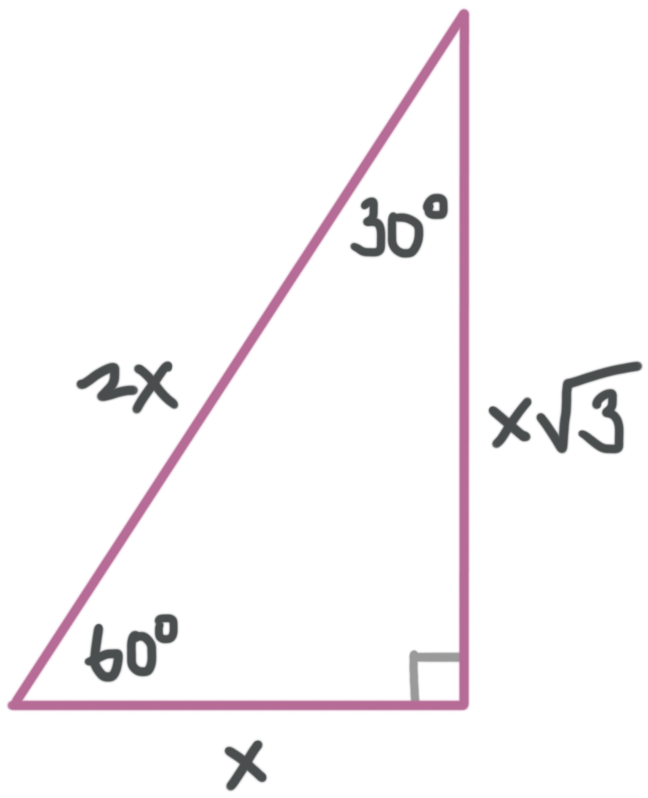



How To Solve 30 60 90 Triangles Krista King Math Online Math Tutor
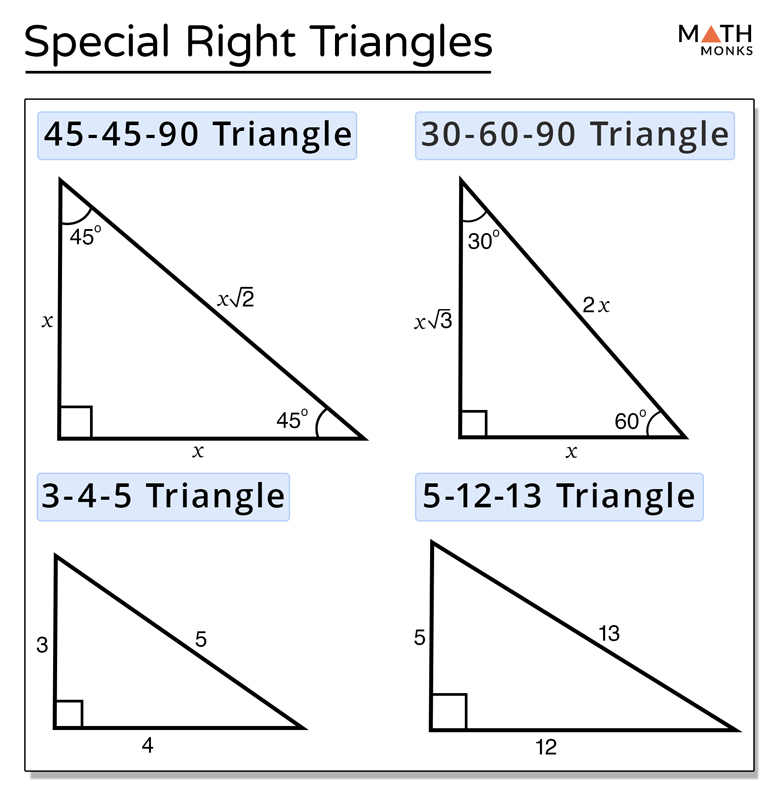



Special Right Triangles Definition Formula Examples




30 60 90 Triangle Definition Theorem Formula Examples




The Complete Guide To The 30 60 90 Triangle
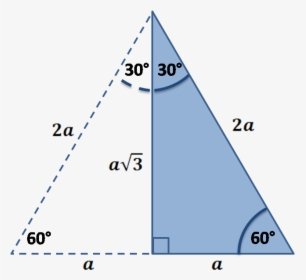



Using The Properties Of The Equilateral Triangle 30 60 90 Triangle Solver Hd Png Download Kindpng




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



The Easy Guide To The 30 60 90 Triangle
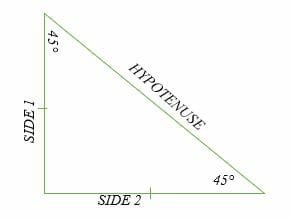



45 45 90 Triangle Explanation Examples




The 30 60 90 Triangle Topics In Trigonometry




5 30 60 90 Triangles Geometry15a



0 件のコメント:
コメントを投稿