[新しいコレクション] 90 60 30 triangle formula 188313-30 60 and 90 triangle formula radical

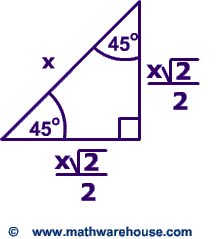
Using what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected itemB) 95°, 30°, 55° c) °, 45°, 46° d) 90°, 60°, 30° Solution An obtuseangled triangle has one of the vertex angles as an obtuse angle (> 90°) Among the given options, option (b) satisfies the condition Therefore, option b ie 95°, 30°, 55° forms an obtuse triangleA triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 What is the formula for a

30 60 90 Triangles

30 60 and 90 triangle formula radical

【印刷可能】 30 60 90 right triangle calculator 649842-30 60 90 right triangle calculator

 We can see that this must be a triangle because we can see that this is a right triangle with one given measurement, 30° The unmarked angle must then be 60° Since 18 is the measure opposite the 60° angle, it must be equal to $x√3$Right Triangle Calculator Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles , the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesIn a 30 60 90 special right triangle the hypotenuse is always equal to twice

Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

30 60 90 right triangle calculator

上 pythagorean theorem 30 60 90 triangle 316555-Pythagorean theorem 30 60 90 triangle

Now let's draw a mirror image of our triangle Next, we can label the length of the new side opposite 30º "a," and About Triangle A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric featuresThis allows us to find the ratio between each side of the triangle by using the Pythagorean theorem Check it out below!

Right S And Trigonometry 7 Pythagorean Theorem The Determine Right Triangles 6 Pythagorean Theorem Solve Sides 5 Wp Pythagorean Theorem 4 Special Right Ppt Download

Pythagorean theorem 30 60 90 triangle